题目内容
19．
如图，已知∠1=50°，∠2=130°，且BD∥CE，AC与DF平行吗？为什么？
分析 由BD∥CE，∠1=50°，利用平行线的性质可得，∠C=∠1=50°，由∠2=130°，可得∠CED=130°，由平行线的判定定理可得AC∥DF．
解答 解：平行．
∵BD∥CE，∠1=50°，
∴∠C=∠1=50°，
∵∠2=130°，
∴∠CED=130°，
∴∠C+∠CED=180°，
∴AC∥DF．
点评 本题主要考查了平行线的性质及判定定理，综合运用平行线的性质和判定定理是解答此题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
7．勾股定理是几何中的一个重要定理．而在西方，则是由著名数学家毕达哥拉斯用如图①的图形验证了勾股定理．故图①由此得名“毕达哥拉斯树”．图②是由图①放入长方形内得到的，∠BAC=90°，∠ABC=30°，BC=4，D、E、F、G、H、I都在长方形KLMJ的边上，则此长方形KLMJ的面积为（ ）
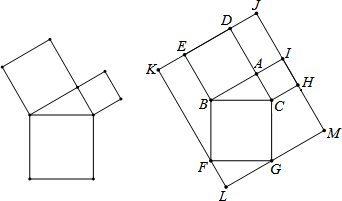
| A． | 48+20$\sqrt{3}$ | B． | 32+20$\sqrt{3}$ | C． | 52+16$\sqrt{3}$ | D． | 28+16$\sqrt{3}$ |
14．
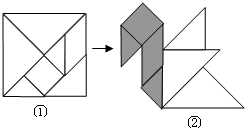用正方形纸板制成一副七巧板，如图①，将它拼成“小天鹅”图案，如图②，若其中阴影部分的面积为6，则正方形纸板的面积为（ ）
用正方形纸板制成一副七巧板，如图①，将它拼成“小天鹅”图案，如图②，若其中阴影部分的面积为6，则正方形纸板的面积为（ ）| A． | 12 | B． | 16 | C． | 18 | D． | 25 |
4．
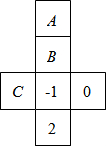如图，是一个正方形盒子的展开图，若要在展开后的其中的三个正方形A、B、C内分别填入适当的数，使得展开图折成正方体后相对的面上的两个数互为相反数，则填入正方形A、B、C内的三个数依次为（ ）
如图，是一个正方形盒子的展开图，若要在展开后的其中的三个正方形A、B、C内分别填入适当的数，使得展开图折成正方体后相对的面上的两个数互为相反数，则填入正方形A、B、C内的三个数依次为（ ）| A． | 1，-2，0 | B． | 0，-2，1 | C． | -2，0，1 | D． | -2，1，0 |
11．某个公司有15名工作人员，他们的月工资情况如下表，则该公司所有工作人员的月工资的中位数和众数分别是（ ）
| 职务 | 经理 | 副经理 | 职员 |
| 人数 | 1 | 2 | 12 |
| 月工资（元） | 5000 | 2000 | 800 |
| A． | 2000，2000 | B． | 800，2000 | C． | 2000，800 | D． | 800，800 |
如图，AB∥DE，CM平分∠BCE，CN⊥CM，猜想∠B与∠DCN的数量关系，并说明理由．
9．若某反比例函数y=$\frac{k}{x}$的图象经过点（3，-4），则该函数图象位于（ ）
| A． | 第一、二象限 | B． | 第二、四象限 | C． | 第一、三象限 | D． | 第三、四象限 |