Question

9．如图，AD∥BC，∠A=90°，AB=BC，点E是AB的中点，BD=CE．
（1）求证：BD⊥CE；
（2）联结CD、DE，试判断△DCE的形状，并证明你的结论．

Answer 1

分析 （1）由条件可证明Rt△ABD≌Rt△BCE，则可求得∠EFD=90°，可证得结论；
（2）过点D作DG⊥BC于G，结合条件可证明△ABD≌△GDB，则可证得BD=CD，结合条件可证得CD=CE，可证明△CDE为等腰三角形．

解答 （1）证明：
∵AD∥BC，
∴∠A+∠CBE=180°，
又∠A=90°，
∴∠CBE=90°；
∵AB=BC，BD=CE，
在Rt△ABD和Rt△BCE中
$\left\{\begin{array}{l}{AB=BC}\\{BD=CE}\end{array}\right.$
∴Rt△ABD≌Rt△BCE（HL），
∴∠D=∠BEC，
∵∠D+∠ABD=90°，
∴∠BEC+∠ABD=90°，
∵∠EFB+∠BEC+∠ABD=180°，
∴∠EFB=90°，
∴BD⊥CE；
（2）解：△DCE是等腰三角形．
证明如下：
∵Rt△ABD≌Rt△BEC，
∴AD=BE，
又AB=BC，
点E是AB的中点，
∴$AD=\frac{1}{2}BC$，
如图，过点D作DG⊥BC于G，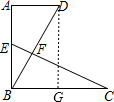

∴∠DGB=90°=∠A，
∵AD∥BC，
∴∠GBD=∠ADB，
在△ABD和△GDB中
$\left\{\begin{array}{l}{∠A=∠DGB}\\{∠ADB=∠GBD}\\{BD=BD}\end{array}\right.$
∴△ABD≌△GDB（AAS），
∴$BG=AD=\frac{1}{2}BC$；
∴DF垂直平分BC，
∴BD=CD，
又BD=CE，
∴CD=CE，
∴△DCE是等腰三角形．

点评 本题主要考查全等三角形的判定和性质，掌握全等三角形的判定和性质是解题的关键，即SSS、SAS、ASA、AAS和HL．