题目内容
10. 如图,在?ABCD中,AB=8,∠C=60°,∠A的平分线与∠B的平分线相交于点E,EF⊥AB,求EF的长.
如图,在?ABCD中,AB=8,∠C=60°,∠A的平分线与∠B的平分线相交于点E,EF⊥AB,求EF的长.
分析 由在?ABCD中,∠C=60°,∠A的平分线与∠B的平分线相交于点E,易证得△ABE是含30°角的直角三角形的性质,继而求得BE的长,又由EF⊥AB,即可求得答案.
解答 解:∵在?ABCD中,∠C=60°,
∴∠DAB=∠C=60°,∠ABC=180°-∠C=120°,
∵∠A的平分线与∠B的平分线相交于点E,
∴∠EAB=$\frac{1}{2}$∠DAB=30°,∠EBA=$\frac{1}{2}$∠ABC=60°,
∴∠AEB=180°-∠EAB-∠EBA=90°,
∵AB=8,EF⊥AB,
∴BE=$\frac{1}{2}$AB=4,
∴EF=BE•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
点评 此题考查了平行四边形的性质以及含30°角的直角三角形的性质.注意证得△ABE是含30°角的直角三角形的性质是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20.下列计算正确的是( )
| A. | a5•a2=a10 | B. | a6÷a2=a3 | C. | a3+a5=a8 | D. | (a2)4=a8 |
5.观察下列一组图形,它反映了图中点的个数与第n图形之间的某种变化规律,
(1)填写下表:
(2)设第n个图形中点的个数为S个,试写出S与n的关系式S=$\frac{1}{2}$(n+1)(n+2);
(3)求出第10个图形中S的值.

(1)填写下表:
| 第n个图形 | 1 | 2 | 3 | 4 |
| 图中所有点的个数 | 3 | 6 | 10 | 15 |
(3)求出第10个图形中S的值.

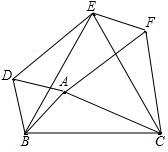 如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF.
如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF.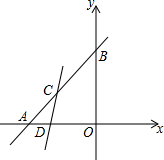 如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1
如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1