题目内容
1.从甲地到乙地全程6km,一段上坡,一段平路,一段下坡,如果保持上坡每小时行2km,平路每小时行3km,下坡每小时行4km,那么,从甲地到乙地需行1小时55分,从乙地到甲地需行2小时25分,求从甲地到乙地上坡、平路、下坡的路程各是多少千米?分析 设甲地到乙地,上坡是x千米,平路是y千米,下坡路是z千米,根据全程6km,从甲地到乙地需行1小时55分,从乙地到甲地需行2小时55分,分别列出方程,组成方程组,再求解即可.
解答 解:设从甲地到乙地上坡是x千米,平路是y千米,下坡路是z千米,根据题意得
$\left\{\begin{array}{l}{x+y+z=6}\\{\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1\frac{11}{12}}\\{\frac{x}{4}+\frac{y}{3}+\frac{z}{2}=2\frac{5}{12}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$.
答:从甲地到乙地上坡是1千米,平路是2千米,下坡路是3千米.
点评 此题考查了三元一次方程组的应用,解答此题的关键是找出题目中的等量关系,列出方程组,用代入消元法或加减消元法求出方程组的解.

练习册系列答案
相关题目
6. 如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )
如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )
 如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )
如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )| A. | $\frac{8}{5}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
13.为了了解一批电视机的使用寿命,从中任意抽取40台电视机进行试验,那么这批电视机中,每台电视机的使用寿命是这个问题的( )
| A. | 个体 | B. | 总体 | C. | 总体的一个样本 | D. | 样本容量 |
 如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.
如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值. 如图,在?ABCD中,AB=8,∠C=60°,∠A的平分线与∠B的平分线相交于点E,EF⊥AB,求EF的长.
如图,在?ABCD中,AB=8,∠C=60°,∠A的平分线与∠B的平分线相交于点E,EF⊥AB,求EF的长.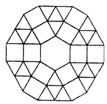 如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.
如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.