题目内容
2.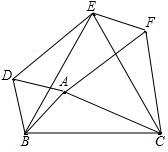 如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF.
如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF.(1)求证:四边形ADEF是平行四边形;
(2)△ABC满足什么条件时,四边形ADEF是菱形?是矩形?并说明理由;
(3)这样的平行四边形ADEF是否总是存在?请说明理由.
分析 (1)根据等边三角形的性质得出AC=AF,AB=BD,BC=BE,∠EBC=∠ABD=60°,求出∠DBE=∠ABC,根据SAS推出△DBE≌△ABC,根据全等得出DE=AC,求出DE=AF,同理AD=EF,根据平行四边形的判定推出即可;
(2)当AB=AC时,四边形ADEF是菱形,根据菱形的判定推出即可;当∠BAC=150°时,四边形ADEF是矩形,求出∠DAF=90°,根据矩形的判定推出即可;
(3)这样的平行四边形ADEF不总是存在,当∠BAC=60°时,此时四边形ADEF就不存在.
解答 (1)证明:∵△ABD、△BCE和△ACF是等边三角形,
∴AC=AF,AB=BD,BC=BE,∠EBC=∠ABD=60°,
∴∠DBE=∠ABC=60°-∠EBA,
在△DBE和△ABC中
$\left\{\begin{array}{l}{BD=BA}\\{∠DBE=∠ABC}\\{BE=BC}\end{array}\right.$
∴△DBE≌△ABC,
∴DE=AC,
∵AC=AF,
∴DE=AF,
同理AD=EF,
∴四边形ADEF是平行四边形;
(2)解:当AB=AC时,四边形ADEF是菱形,
理由是:∵△ABD和△AFC是等边三角形,
∴AB=AD,AC=AF,
∵AB=AC,
∴AD=AF,
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形;
当∠BAC=150°时,四边形ADEF是矩形,
理由是:∵△ABD和△ACF是等边三角形,
∴∠DAB=∠FAC=60°,
∵∠BAC=150°,
∴∠DAF=90°,
∵四边形ADEF是平行四边形,
∴四边形ADEF是矩形;
(3)解:这样的平行四边形ADEF不总是存在,
理由是:当∠BAC=60°时,∠DAF=180°,
此时点D、A、F在同一条直线上,此时四边形ADEF就不存在.
点评 本题考查了菱形的判定,矩形的判定,平行四边形的判定,等边三角形的性质,全等三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键,题目比较好,难度适中.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | 个体 | B. | 总体 | C. | 总体的一个样本 | D. | 样本容量 |
 如图,在?ABCD中,AB=8,∠C=60°,∠A的平分线与∠B的平分线相交于点E,EF⊥AB,求EF的长.
如图,在?ABCD中,AB=8,∠C=60°,∠A的平分线与∠B的平分线相交于点E,EF⊥AB,求EF的长.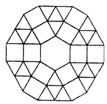 如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.
如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.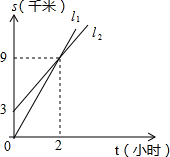 A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断:
A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断: