题目内容
6.已知x(2x-y)=y(y-2x)(xy≠0),求$\frac{{x}^{2}+{y}^{2}}{xy}$的值.分析 首先利用因式分解法得出(2x-y)(x+y)=0,求得x、y之间的关系,进一步代入求得答案即可.
解答 解:∵x(2x-y)=y(y-2x)(xy≠0),
∴(2x-y)(x+y)=0,
∴2x-y=0,x+y=0,
∴y=2x,或x=-y,
当y=2x时,$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{{x}^{2}+4{x}^{2}}{x•2x}$=$\frac{5}{2}$;
当x=-y时,$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{2{x}^{2}}{-{x}^{2}}$=-2.
点评 此题考查因式分解的实际运用,掌握因式分解的方法和代换代入是解决问题的关键.

练习册系列答案
相关题目
14.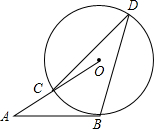 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )
 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )| A. | 25° | B. | 30° | C. | 35° | D. | 45° |
16.若m=$\sqrt{40}$-5,则估计m的值所在的范围是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |




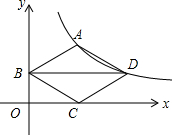 如图,菱形ABCD的对角线BD与x轴平行,点B、C的坐标分别是(0,1)、(2,0),点A、D在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为4.
如图,菱形ABCD的对角线BD与x轴平行,点B、C的坐标分别是(0,1)、(2,0),点A、D在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为4.