题目内容
18.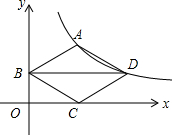 如图,菱形ABCD的对角线BD与x轴平行,点B、C的坐标分别是(0,1)、(2,0),点A、D在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为4.
如图,菱形ABCD的对角线BD与x轴平行,点B、C的坐标分别是(0,1)、(2,0),点A、D在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为4.
分析 连结AC,如图,根据菱形的性质得AC与BD互相垂直平分,再利用BD∥x轴得到AC⊥x轴,则可写出A点坐标,然后根据反比例函数图象上点的坐标特征求k的值.
解答 解:连结AC,如图,
∵四边形ABCD为菱形,
∴AC与BD互相垂直平分,
∵BD∥x轴,
∴AC⊥x轴,
∴A点坐标为(2,2),
∴k=2×2=4.
故答案为4.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目

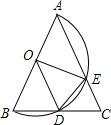 如图,△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E.
如图,△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E.