题目内容
17．
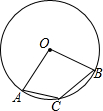已知：如图，OA、OB是⊙O的两条半径，且OA⊥OB，点C是劣弧AB上一点，则∠ACB的度数为（ ）| A． | 120° | B． | 135° | C． | 150° | D． | 不能确定 |
分析 首先在优弧AB上取点D，连接AD，BD，由圆周角定理即可求得∠ADB的度数，然后由圆的内接四边形的性质，求得∠ACB的度数．
解答 
解：在优弧AB上取点D，连接AD，BD，
∵OA⊥OB，
∴∠AOB=90°，
∴∠ADB=$\frac{1}{2}$∠AOB=45°，
∴∠ACB=180°-∠ADB=135°．
故选B．
点评 此题考查了圆周角定理以及圆的内接四边形的性质．注意准确作出辅助线是解此题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
12．
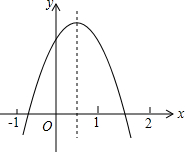二次函数y=ax2+bx+c的图象如图所示，则下列式子
①abc＜0；②a＜$\frac{c-b}{2}$；③0＜b＜-2a；④a-b+c＜0中，
成立的个数有（ ）
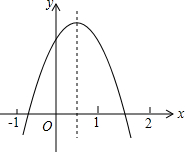二次函数y=ax2+bx+c的图象如图所示，则下列式子①abc＜0；②a＜$\frac{c-b}{2}$；③0＜b＜-2a；④a-b+c＜0中，
成立的个数有（ ）
| A． | ①④ | B． | ①②④ | C． | ①③④ | D． | ①②③④ |
9．若方程（m-1）${x}^{{m}^{2}+1}$+2mx-3=0是关于x的一元二次方程，则m的值（ ）
| A． | 1 | B． | -1 | C． | ±1 | D． | 2 |
如图，AD为△ABC的中线，BE为△ABD中线