题目内容
18. 如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )
如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )| A. | $6\sqrt{2}$ | B. | $6\sqrt{3}$ | C. | 8 | D. | 10 |
分析 连接CD,由题意得∠ACD=90°,根据∠ABC=∠DAC,得AC=CD,在等腰直角三角形ACD中,AD=12,根据勾股定理得出AC即可.
解答  解:连接CD,
解:连接CD,
∵直径AD=12,
∴∠ACD=90°,
∵∠ABC=∠DAC,
∴AC=CD,
∴在等腰直角三角形ACD中,∵AD=12,
∴根据勾股定理得AC2+CD2=AD2,
∴AC=6$\sqrt{2}$,
故选A.
点评 本题考查了三角形的外接圆,掌握圆周角定理、直径所对的圆周角等于90°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.函数y=$\left\{\begin{array}{l}{x+1(x<1)}\\{\frac{2}{x}(x≥1)}\end{array}\right.$,当y=a时,对应的x有唯一确定的值,则a的取值范围为( )
| A. | a≤0 | B. | a<0 | C. | 0<a<2 | D. | a≤0或a=2 |
6.已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1<y2≤y0,则x0的取值范围是( )
| A. | -5≤x0-3 | B. | -5≤x0<2 | C. | x0≥-5 | D. | -5≤x0<-1 |
3.对于二项方程axn+b=0(a≠0,b≠0),当n为偶数时,已知方程无实数根,那么ab一定( )
| A. | ab<0 | B. | ab≤0 | C. | ab>0 | D. | ab≥0 |
10. 已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )
 已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )| A. | y<-4 | B. | y<-2 | C. | -2<y<0 | D. | -4<y<0 |
 如图,多边形的相邻两边均互相垂直,则这个多边形的周长为2a+2b.
如图,多边形的相邻两边均互相垂直,则这个多边形的周长为2a+2b.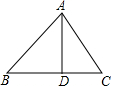 如图,在△ABC中,AD⊥BC交BC于点D,若BC=14,AD=12,tan∠BAD=$\frac{3}{4}$,则DC的长为( )
如图,在△ABC中,AD⊥BC交BC于点D,若BC=14,AD=12,tan∠BAD=$\frac{3}{4}$,则DC的长为( ) 如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.
如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.