题目内容
3.对于二项方程axn+b=0(a≠0,b≠0),当n为偶数时,已知方程无实数根,那么ab一定( )| A. | ab<0 | B. | ab≤0 | C. | ab>0 | D. | ab≥0 |
分析 根据n为偶数时,方程无实数根,得出-$\frac{b}{a}$<0即可.
解答 解:axn+b=0,
可得:xn=$\frac{-b}{a}$,
因为当n为偶数时,方程无实数根,
所以$-\frac{b}{a}<0$,
所以ab>0,
故选C
点评 此题考查高次方程的问题,关键是根据n为偶数时,方程无实数根得出ab的范围.

练习册系列答案
相关题目
11. 如图所示的长方形阴影区域的面积是( )
如图所示的长方形阴影区域的面积是( )
 如图所示的长方形阴影区域的面积是( )
如图所示的长方形阴影区域的面积是( )| A. | 9 | B. | 12 | C. | 14 | D. | 16 |
18. 如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )
如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )
 如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )
如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )| A. | $6\sqrt{2}$ | B. | $6\sqrt{3}$ | C. | 8 | D. | 10 |
12.实数$\sqrt{3}$的相反数是( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{\sqrt{3}}$ | C. | ±$\sqrt{3}$ | D. | -$\sqrt{3}$ |
13.x取何值时,代数式6+2x是负数( )
| A. | x<3 | B. | x≤3 | C. | x<-3 | D. | x>-3 |
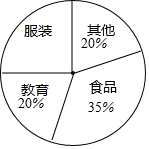 小明家下个月的开支预算如图所示.如果他家用于教育支出约为500元.那么他家下月的总支出约是多少元?用于购买食品、服装的支出分别约是多少元?
小明家下个月的开支预算如图所示.如果他家用于教育支出约为500元.那么他家下月的总支出约是多少元?用于购买食品、服装的支出分别约是多少元?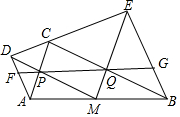 如图,在Rt△ABC中,∠ACB=90°,分别以AC、AB为斜边向△ABC外作等腰直角△ACD和等腰直角△BCE,取AB的中点M,连接MD,ME分别交AC、BC于点P、Q,直线PQ分别交AD、BE于点F、G.有以下结论:①△MDE是等腰直角三角形;②PQ=PF+QG;③△APF∽△EQG;④S△ACD+S△BCE=S△ABC.
如图,在Rt△ABC中,∠ACB=90°,分别以AC、AB为斜边向△ABC外作等腰直角△ACD和等腰直角△BCE,取AB的中点M,连接MD,ME分别交AC、BC于点P、Q,直线PQ分别交AD、BE于点F、G.有以下结论:①△MDE是等腰直角三角形;②PQ=PF+QG;③△APF∽△EQG;④S△ACD+S△BCE=S△ABC.