题目内容
8. 如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.
如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.(1)证明:四边形OCED为菱形;
(2)若AC=4,求四边形CODE的周长.
分析 (1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形CODE是菱形,
(2)求出OC=OD=2,由菱形的性质即可得出答案.
解答 (1)证明:∵CE∥BD,DE∥AC,
∴四边形CODE为平行四边形
又∵四边形 ABCD 是矩形
∴OD=OC
∴四边形CODE为菱形;
(2)解:∵四边形 ABCD 是矩形
∴OC=OD=$\frac{1}{2}$AC
又∵AC=4
∴OC=2
由(1)知,四边形CODE为菱形
∴四边形CODE的周长为=4OC=2×4=8.
点评 此题考查了矩形的性质、菱形的判定与性质等知识,熟练掌握菱形的判定方法是解题的关键.

练习册系列答案
相关题目
18. 如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )
如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )
 如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )
如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=△DAC,则AC的长为( )| A. | $6\sqrt{2}$ | B. | $6\sqrt{3}$ | C. | 8 | D. | 10 |
19.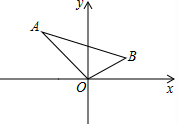 如图,点A、B的坐标分别为(-5,6)、(3,2),则三角形ABO的面积为( )
如图,点A、B的坐标分别为(-5,6)、(3,2),则三角形ABO的面积为( )
 如图,点A、B的坐标分别为(-5,6)、(3,2),则三角形ABO的面积为( )
如图,点A、B的坐标分别为(-5,6)、(3,2),则三角形ABO的面积为( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
13.x取何值时,代数式6+2x是负数( )
| A. | x<3 | B. | x≤3 | C. | x<-3 | D. | x>-3 |
18. 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )| A. | 四边形ACDF是平行四边形 | |
| B. | 当点E为BC中点时,四边形ACDF是矩形 | |
| C. | 当点B与点E重合时,四边形ACDF是菱形 | |
| D. | 四边形ACDF不可能是正方形 |
 如图,BD⊥AC于D,EF⊥AC于F,MD∥BC,∠1=∠2.
如图,BD⊥AC于D,EF⊥AC于F,MD∥BC,∠1=∠2.