题目内容
19.解三元一次方程组:(1)$\left\{\begin{array}{l}{3x-y+z=4}\\{2x+3y-z=12}\\{x+y+z=6}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+z-3=0}\\{2x-y+2z=2}\\{x-y-z=-3}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-y+z=4①}\\{2x+3y-z=12②}\\{x+y+z=6③}\end{array}\right.$,
①+②得:5x+2y=16④,
②+③得:3x+4y=18⑤,
④×2-⑤得:7x=14,即x=2,
把x=2代入④得:y=3,
把x=2,y=3代入③得:z=1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+z-3=0①}\\{2x-y+2z=2②}\\{x-y-z=-3③}\end{array}\right.$,
②-③得:x+3z=5④,
④-①得:2z=2,即z=1,
把z=1代入④得:x=2,
把z=1,x=2代入③得:y=4,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=4}\\{z=1}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.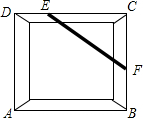 如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )
如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )
 如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )
如图,利用所学的知识进行逻辑推理,工人盖房时常用木条EF固定矩形门框ABCD,使其不变形这种做法的根据是( )| A. | 两点之间线段最短 | B. | 矩形的对称性 | ||
| C. | 矩形的四个角都是直角 | D. | 三角形的稳定性 |
 如图,平行四边形ABCD中,BC=2AB,点M为AD的中点,则∠BMC=90°.
如图,平行四边形ABCD中,BC=2AB,点M为AD的中点,则∠BMC=90°.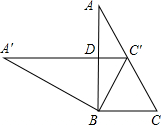 如图,两块相同的三角形完全重合在一起,∠A=30°,AC=12,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C在AC上,A′C与AB相交于点D,则C′D=3.
如图,两块相同的三角形完全重合在一起,∠A=30°,AC=12,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C在AC上,A′C与AB相交于点D,则C′D=3. 如图,若△ABC∽△AED,AD=10cm,BD=12cm,AC=12cm,则AE=$\frac{55}{3}$cm.
如图,若△ABC∽△AED,AD=10cm,BD=12cm,AC=12cm,则AE=$\frac{55}{3}$cm. 如图.∠A0B上有C,D两点,过C作CE⊥OA交0B于E,过D作DF⊥0B交OA于F.求证:C,D,E,F四点在同一圆上.
如图.∠A0B上有C,D两点,过C作CE⊥OA交0B于E,过D作DF⊥0B交OA于F.求证:C,D,E,F四点在同一圆上.