题目内容
10.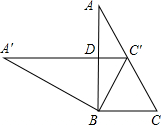 如图,两块相同的三角形完全重合在一起,∠A=30°,AC=12,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C在AC上,A′C与AB相交于点D,则C′D=3.
如图,两块相同的三角形完全重合在一起,∠A=30°,AC=12,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C在AC上,A′C与AB相交于点D,则C′D=3.
分析 根据含30度的直角三角形三边的关系,在Rt△ABC中得到BC=$\frac{1}{2}$AC=6,利用互余得到∠C=60°,再根据旋转的性质得BC′=BC=6,∠BC′A=∠C=60°,则可判断△BCC′为等边三角形,所以∠CBC′=60°,于是有∠ABC=30°,∠BDC′=90°,然后在Rt△BDC′中根据含30度的直角三角形三边的关系易得C′D的长.
解答 解:在Rt△ABC中,∵∠A=30°,
∴BC=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6,∠C=60°,
∵△ABC绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,
∴BC′=BC=6,∠BC′A=∠C=60°,
∴△BCC′为等边三角形,
∴∠CBC′=60°,
∴∠ABC=90°-60°=30°,
∴∠BDC′=90°,
在Rt△BDC′中,∵∠DBC′=30°,
∴C′D=$\frac{1}{2}$BC′=$\frac{1}{2}$×6=3.
故答案为3.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15. 如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
 如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )| A. | 40° | B. | 30° | C. | 20° | D. | 50° |
2. 如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3 A2B2,顶点P3在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为( )
如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3 A2B2,顶点P3在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为( )
 如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3 A2B2,顶点P3在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为( )
如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3 A2B2,顶点P3在反比例函数y=$\frac{2}{x}$ (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为( )| A. | ($\sqrt{3}+1$,$\sqrt{3}-1$) | B. | ($\sqrt{5}+1$,$\sqrt{5}-1$) | C. | ($\sqrt{3}-1$,$\sqrt{3}+1$) | D. | ($\sqrt{5}-1$,$\sqrt{5}+1$) |
 如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是点N.
如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是点N.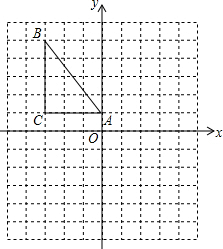 如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,在如图的坐标系中,点A的坐标为(0,1),点B的坐标为(-3,5),AC与x轴平行.
如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,在如图的坐标系中,点A的坐标为(0,1),点B的坐标为(-3,5),AC与x轴平行.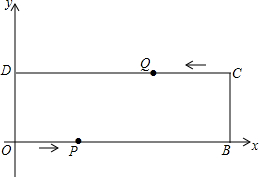 已知长方形的生活小区OBCD的边长分别为40米和130米,如图,建立平面直角坐标系,“创文明城市”宣传车点P从点O出发,沿OB运动至点B停止,宣传车点Q从点C出发,沿CD运动至点D停止,两车同时出发,速度都是1米/秒;宣传车音响半径可达25米,(两点间距离公式:|AB|=$\sqrt{({x}_{A}-{x}_{B})^{2}+({y}_{A}-{y}_{B})^{2}}$)
已知长方形的生活小区OBCD的边长分别为40米和130米,如图,建立平面直角坐标系,“创文明城市”宣传车点P从点O出发,沿OB运动至点B停止,宣传车点Q从点C出发,沿CD运动至点D停止,两车同时出发,速度都是1米/秒;宣传车音响半径可达25米,(两点间距离公式:|AB|=$\sqrt{({x}_{A}-{x}_{B})^{2}+({y}_{A}-{y}_{B})^{2}}$)