题目内容
6.已知关于x的一元二次方程x2-2kx+k2+2=2(1-x)有两个实数根x1,x2.(1)求实数k的取值范围;
(2)若方程的两实根x1,x2满足|x1+x2|=x1x2-1,求k的值.
分析 (1)根据方程有两个实数根可以得到△≥0,从而求得k的取值范围;
(2)利用根与系数的关系将两根之和和两根之积代入代数式求k的值即可.
解答 解:x2-2kx+k2+2=2(1-x),
整理得x2-(2k-2)x+k2=0.
(1)∵方程有两个实数根x1,x2.
∴△=(2k-2)2-4k2≥0,
解得k≤$\frac{1}{2}$;
(2)由根与系数关系知:
x1+x2=2k-2,x1x2=k2,
又|x1+x2|=x1x2-1,代入得,
|2k-2|=k2-1,
∵k≤$\frac{1}{2}$,
∴2k-2<0,
∴|2k-2|=k2-1可化简为:k2+2k-3=0.
解得k=1(不合题意,舍去)或k=-3,
∴k=-3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.以及根与系数的关系.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
16.下列各式计算正确的是( )
| A. | $\sqrt{{2}^{2}+{3}^{2}}$=2+3 | B. | 3$\sqrt{2}$+5$\sqrt{3}$=8$\sqrt{6}$ | ||
| C. | $\sqrt{1{5}^{2}-1{2}^{2}}$=$\sqrt{15+12}$×$\sqrt{15-12}$ | D. | $\sqrt{4\frac{1}{2}}$=2$\sqrt{\frac{1}{2}}$ |
 如图,Rt△ABC中,∠C=90°,作∠BAD=∠BAC交CB的延长线于D,若BC=3cm,则点B到直线AD的距离等于3cm.
如图,Rt△ABC中,∠C=90°,作∠BAD=∠BAC交CB的延长线于D,若BC=3cm,则点B到直线AD的距离等于3cm.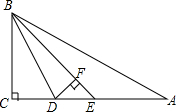 如图,在直角三角形ABC中,∠C=90°,BD是△ABC的角平分线,BE是△BDA的角平分线,DF是△BDE的高线,已知∠DBE=15°,求∠A和∠EDF的度数.
如图,在直角三角形ABC中,∠C=90°,BD是△ABC的角平分线,BE是△BDA的角平分线,DF是△BDE的高线,已知∠DBE=15°,求∠A和∠EDF的度数.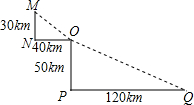 如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是5000万元/km,该沿江高速公路的造价预计是多少?
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三个城市的沿江高速公路,已知该沿江高速公路的建设成本是5000万元/km,该沿江高速公路的造价预计是多少?