题目内容
3．当m为任意实数时，方程2x2-mx-4=0一定有两个不相等的实数根．分析 首先根据题意求得判别式△=m2+32＞0，然后根据非负数的性质求得答案．
解答 解：∵a=2，b=m，c=-4，
∴△=b2-4ac=m2-4×2×（-4）=m2+32，
∵m2≥0，
∴m2+32＞0，
则m的值可以是任意实数，
当m为任意实数时，方程2x2-mx-4=0一定有两个不相等的实数根．
故答案为：任意实数．
点评 此题考查了一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根．
练习册系列答案
阅读快车系列答案
相关题目
如图，△PQR的外角∠PRN的平分线PM与内角∠PQR的平分线QM交于点M，∠QMR=40°，则∠RPM的度数为50°．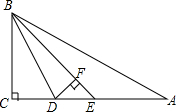
如图，在直角三角形ABC中，∠C=90°，BD是△ABC的角平分线，BE是△BDA的角平分线，DF是△BDE的高线，已知∠DBE=15°，求∠A和∠EDF的度数．