题目内容
 如图,点E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE的位置.若AE=1,BE=2,CE=3,则求∠BE′C的度数.(提示:连接EE′)
如图,点E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE的位置.若AE=1,BE=2,CE=3,则求∠BE′C的度数.(提示:连接EE′)考点:旋转的性质,勾股定理的逆定理,等腰直角三角形,正方形的性质
专题:计算题
分析:连接EE′,如图,根据旋转的性质得BE=BE′=2,AE=CE′=1,∠EBE′=90°,则可判断△BEE′为等腰直角三角形,根据等腰直角三角形的性质得EE′=
BE=2
,∠BE′E=45°,在△CEE′中,由于CE′2+EE′2=CE2,根据勾股定理的逆定理得到△CEE′为直角三角形,即∠EE′C=90°,然后利用∠BE′C=∠BE′E+∠CE′E求解.
| 2 |
| 2 |
解答: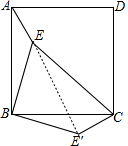 解:连接EE′,如图,
解:连接EE′,如图,
∵△ABE绕点B顺时针旋转90°得到△CBE′,
∴BE=BE′=2,AE=CE′=1,∠EBE′=90°,
∴△BEE′为等腰直角三角形,
∴EE′=
BE=2
,∠BE′E=45°,
在△CEE′中,CE=3,CE′=1,EE′=2
,
∵12+(2
)2=32,
∴CE′2+EE′2=CE2,
∴△CEE′为直角三角形,
∴∠EE′C=90°,
∴∠BE′C=∠BE′E+∠CE′E=135°.
 解:连接EE′,如图,
解:连接EE′,如图,∵△ABE绕点B顺时针旋转90°得到△CBE′,
∴BE=BE′=2,AE=CE′=1,∠EBE′=90°,
∴△BEE′为等腰直角三角形,
∴EE′=
| 2 |
| 2 |
在△CEE′中,CE=3,CE′=1,EE′=2
| 2 |
∵12+(2
| 2 |
∴CE′2+EE′2=CE2,
∴△CEE′为直角三角形,
∴∠EE′C=90°,
∴∠BE′C=∠BE′E+∠CE′E=135°.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理的逆定理、等腰直角三角形的判定与性质和正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.求证:BD=BE.
如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.求证:BD=BE. 在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.