题目内容
3. 如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )
如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )| A. | (1,$\sqrt{3}$) | B. | (-1,-$\sqrt{3}$) | C. | (1,-$\sqrt{3}$) | D. | (-1,$\sqrt{3}$) |
分析 由于2017=6×336+1,则可判断第2017秒时,点P运动到点C,作CH⊥x轴于H,如图,根据正六边形的性质得到OB=BC=1,∠BCD=120°,所以∠BCH=30°,再通过解直角三角形求出CH和BH,然后写出C点坐标即可.
解答 解:∵2017=6×336+1,
∴第2017秒时,点P运动到点C,
作CH⊥x轴于H,如图,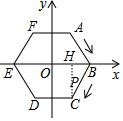
∵六边形ABCDEF是半径为1的正六边形,
∴OB=BC=2,∠BCD=120°,
∴∠BCH=30°,
在Rt△BCH中,BH=$\frac{1}{2}$BC=1,CH=$\sqrt{3}$BH=$\sqrt{3}$,
∴OH=OB-BH=1,
∴C点坐标为(1,-$\sqrt{3}$),
∴第2017秒时,点P的坐标是(1,-$\sqrt{3}$).
故选C.
点评 本题考查了规律型:点的坐标:利用正多边形的性质确定动点的运动规律,熟记正多边形以及解直角三角形的有关知识是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( )
 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( )| A. | 9.5° | B. | 19° | C. | 15° | D. | 30° |
8.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
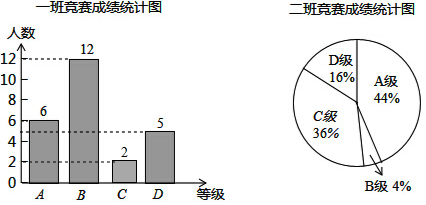
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有21人;
(2)补全下表中空缺的三个统计量:
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有21人;
(2)补全下表中空缺的三个统计量:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | 77.6 | 80 | 80 |
| 二班 | 77.6 | 70 | 90 |
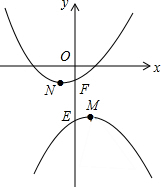 如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
 将下列各选项中的平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
将下列各选项中的平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )



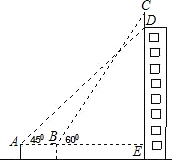 如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)
如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)