题目内容
18. 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( )| A. | 9.5° | B. | 19° | C. | 15° | D. | 30° |
分析 先根据平行线的性质求出∠AED与∠DEB的度数,再由角平分线的性质求出∠DEF的度数,进而可得出∠GEF的度数,再根据三角形外角的性质即可得出结论.
解答 解:∵AB∥CD,∠CDE=119°,
∴∠AED=180°-119°=61°,∠DEB=119°.
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=$\frac{1}{2}$×119°=59.5°,
∴∠GEF=61°+59.5°=120.5°.
∵∠AGF=130°,
∴∠F=∠AGF-∠GEF=130°-120.5°=9.5°.
故选:A.
点评 本题考查的是平行线的性质,解题时注意:两直线平行,同旁内角互补,内错角相等.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.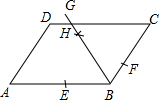 如图,在?ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )
如图,在?ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )
 如图,在?ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )
如图,在?ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )| A. | BG平分∠ABC | B. | BE=BF | C. | AD=CH | D. | CH=DH |
3. 如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )
如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )
 如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )
如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )| A. | (1,$\sqrt{3}$) | B. | (-1,-$\sqrt{3}$) | C. | (1,-$\sqrt{3}$) | D. | (-1,$\sqrt{3}$) |
 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且$\widehat{AE}=\widehat{DE}$,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且$\widehat{AE}=\widehat{DE}$,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.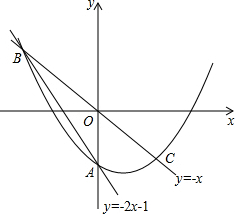 在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.
在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.
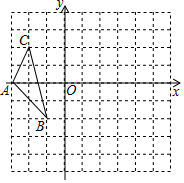 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:
如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为: 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,则EF=5cm.
如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,则EF=5cm.