题目内容
6.直角三角形的两个锐角平分线与斜边的所夹的锐角之和是( )| A. | 30° | B. | 60° | C. | 45° | D. | 15°和75° |
分析 根据题意画出图形,先根据直角三角形的性质求出∠BAC+∠ABC=90°,再由角平分线的定义即可得出结论.
解答  解:如图,∠C=90°,BP,AP是两个锐角的平分线交于点P,
解:如图,∠C=90°,BP,AP是两个锐角的平分线交于点P,
∵∠C=90°,
∴∠BAC+∠ABC=90°
∴$\frac{1}{2}$(∠BAC+∠ABC)=45°.
∵BD平分∠ABC,AP平分∠BAC,
∴∠BAP=$\frac{1}{2}$∠BAC,∠ABP=$\frac{1}{2}$∠ABC,
∴直角三角形的两个锐角平分线所夹的锐角=∠BAP+∠ABP=45°.
故选C.
点评 本题考查的是三角形内角和定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.满足等式:(-2)3•(-2)x=-$\frac{1}{32}$的x的值为( )
| A. | -8 | B. | -5 | C. | 5 | D. | 3 |
14.在直角坐标系xOy中,已知P(m,n),m、n满足(m2+1+n2)(m2+4+n2)=10,则OP的长( )
| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{6}$或1 | D. | 1 |
11.分解因式(2x+3)2-x2的结果是( )
| A. | 3(x2+4x+3) | B. | 3(x2+2x+3) | C. | (3x+3)(x+3) | D. | 3(x+1)(x+3) |
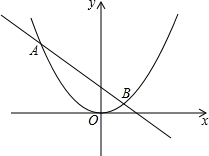 已知抛物线y=$\frac{1}{4}$x2与直线y=$-\frac{3}{4}$x+1交于A、B两点(A在B的左侧)
已知抛物线y=$\frac{1}{4}$x2与直线y=$-\frac{3}{4}$x+1交于A、B两点(A在B的左侧)