题目内容
17．已知m是方程x2+x-1=0的一个根，求代数式（m+1）2+（m+1）（m-1）的值．分析 由m为已知方程的解，将x=m代入方程求出m2+m的值，原式整理后代入计算即可求出值．
解答 解：把x=m代入方程得：m2+m-1=0，即m2+m=1，
则原式=m2+2m+1+m2-1=2（m2+m）=2．
点评 此题考查了一元二次方程的解，方程的解即为能使方程左右两边相等的未知数的值．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
16．
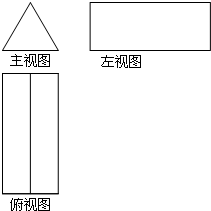如图是几何体的三视图，该几何体是（ ）
如图是几何体的三视图，该几何体是（ ）| A． | 正三棱柱 | B． | 正三棱锥 | C． | 圆锥 | D． | 圆柱 |
17．已知反比例函数y=-$\frac{3}{x}$，下列结论不正确的是（ ）
| A． | 图象必经过点（-1，3） | B． | 两个分支分布在第二、四象限 | ||
| C． | 若x＞1，则-3＜y＜0 | D． | y随x的增大而增大 |
5．在-$\frac{5}{3}$，-$\sqrt{2}$，-$\sqrt{3}$，-$\frac{π}{2}$四个数中，最大的数是（ ）
| A． | -$\frac{5}{3}$ | B． | -$\sqrt{2}$ | C． | -$\sqrt{3}$ | D． | -$\frac{π}{2}$ |
12．
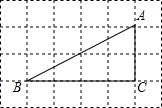如图，△ABC的顶点都是正方形网格中的格点，则cosA等于（ ）
如图，△ABC的顶点都是正方形网格中的格点，则cosA等于（ ）| A． | $\frac{2\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\sqrt{5}$ | D． | $\frac{2}{3}$ |
2．若a为有理数，则（a3）2的值为（ ）
| A． | 有理数 | B． | 正数 | C． | 零或负数 | D． | 正数或零 |
7．在△ABC中，∠A=90°，AB=3，BC=5，则sinB的值是（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{5}$ |