��Ŀ����
11��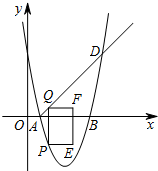 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+5��x�ύ��A��1��0����B��5��0�����㣬��D���������Ϻ�����Ϊ6�ĵ㣮��P�������������ϣ��Ҳ���A��D�����غϣ�����P��y���ƽ����������AD���ڵ�Q������Q��QF��ֱ��y�ᣬ��F�ڵ�Q���Ҳ࣬��QF=2����QF��QPΪ�ڱ�������QPEF�������QPEF���ܳ�Ϊd����P�ĺ�����Ϊm��
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+5��x�ύ��A��1��0����B��5��0�����㣬��D���������Ϻ�����Ϊ6�ĵ㣮��P�������������ϣ��Ҳ���A��D�����غϣ�����P��y���ƽ����������AD���ڵ�Q������Q��QF��ֱ��y�ᣬ��F�ڵ�Q���Ҳ࣬��QF=2����QF��QPΪ�ڱ�������QPEF�������QPEF���ܳ�Ϊd����P�ĺ�����Ϊm����1������������������Ӧ�ĺ�������ʽ��
��2�������������ߵĶԳ��Ὣ����QPEF�������Ϊ1��2������ʱm��ֵ��
��3����d��m֮��ĺ�����ϵʽ��d��m���������Сʱd��ȡֵ��Χ��
��4��������QPEF�ĶԽ����ഹֱʱ��ֱ��д����Գ����ĵĺ����꣮
���� ��1��ֱ�����ô���ϵ����������κ�������ʽ���ɣ�
��2��������������Գ�������ó�m��ֵ��
��3���ֱ����õ�1��m��6ʱ��d=2��-m2+7m-6+2������m��6ʱ��d=2��m2-7m+6+2�����d��ȡֵ��Χ���ɣ�
��4��������QPEF�ĶԽ����ഹֱʱ�������QPEF�������Σ��߳�Ϊ2�������ó�m��ֵ����𰸣�
��� �⣺��1����A��1��0����B��5��0������y=ax2+bx+5��
$\left\{\begin{array}{l}{a+b+5=0}\\{25a+5b+5=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$��
��y=x2-6x+5��
��2����ͼ��ʾ����������y=x2-6x+5�ĶԳ���Ϊ��x=-$\frac{b}{2a}$=-$\frac{-6}{2}$=3��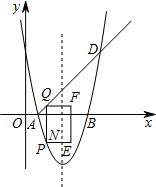
�����������ߵĶԳ��Ὣ����QPEF�������Ϊ1��2�����֣�
�ɵ�PN=3-m��PE=2��
��$\frac{3-m}{2}$=$\frac{2}{3}$��$\frac{3-m}{2}$=$\frac{1}{3}$��
��ã�m=$\frac{5}{3}$��m=$\frac{7}{3}$��
��3����x=6ʱ��y=x2-6x+5=62-6��6+5=5��
���D��������6��5����
����AD����Ӧ�ĺ�������ʽΪy=x-1��x��1����
��P��m��m2-6m+5����Q��m��m-1����
��1��m��6ʱ��d=2��-m2+7m-6+2��=-2m2+14m-8��
��m��6ʱ��d=2��m2-7m+6+2��=2m2-14m+16��
��d=-2m2+14m-8=-2��m-$\frac{7}{2}$��2+$\frac{33}{2}$��
��d��m���������Сʱd��ȡֵ��Χ��4��d��$\frac{33}{2}$��
��4��������QPEF�ĶԽ����ഹֱʱ�������QPEF�������Σ��߳�Ϊ2��
��1��m��6ʱ��m-1-��m2-6m+5��=2��
�����ã�m2-7m+8=0��
��ã�m1=$\frac{7+\sqrt{17}}{2}$��m2=$\frac{7-\sqrt{17}}{2}$��
��m��6ʱ��m2-6m+5-��m-1��=2��
�����ã�m2-7m+4=0��
��ã�m3=$\frac{7+\sqrt{33}}{2}$��m4=$\frac{7-\sqrt{33}}{2}$����ȥ����
����Գ����ĵĺ�����Ϊ��$\frac{7+\sqrt{17}}{2}$+1=$\frac{9+\sqrt{17}}{2}$��$\frac{7-\sqrt{17}}{2}$+1=$\frac{9-\sqrt{17}}{2}$��$\frac{7+\sqrt{33}}{2}$+1=$\frac{9+\sqrt{33}}{2}$��
���� ������Ҫ�����˶��κ����ۺ��Լ������ε����ʵ�֪ʶ�����������ʾ������QPEF�ı߳��ǽ���ؼ���

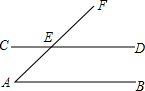 ��ͼ��ֱ��AB��CD��AF��CD�ڵ�E����CEA=45�㣬���A���ڣ�������
��ͼ��ֱ��AB��CD��AF��CD�ڵ�E����CEA=45�㣬���A���ڣ�������| A�� | 35�� | B�� | 45�� | C�� | 50�� | D�� | 135�� |
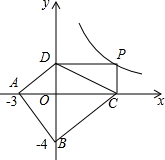 ��ͼ����֪A��-3��0����B��0��-4����PΪ����������y=$\frac{12}{x}$��x��0��ͼ���ϵĶ��㣬PC��x����C��PD��y����D�����ı���ABCD�������СֵΪ��������
��ͼ����֪A��-3��0����B��0��-4����PΪ����������y=$\frac{12}{x}$��x��0��ͼ���ϵĶ��㣬PC��x����C��PD��y����D�����ı���ABCD�������СֵΪ��������| A�� | 12 | B�� | 13 | C�� | 24 | D�� | 26 |
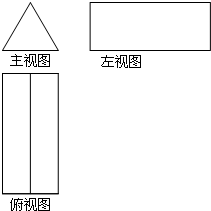 ��ͼ�Ǽ����������ͼ���ü������ǣ�������
��ͼ�Ǽ����������ͼ���ü������ǣ�������| A�� | �������� | B�� | ������ | C�� | Բ | D�� | Բ�� |
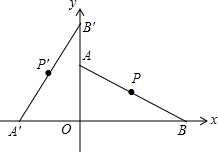 ��ͼ����ƽ��ֱ������ϵ�У�A��0��$2\sqrt{3}$����B��6��0������PΪ�߶�AB���е㣬���߶�AB�Ƶ�O��ʱ����ת90����P�Ķ�Ӧ��P��������ǣ�������
��ͼ����ƽ��ֱ������ϵ�У�A��0��$2\sqrt{3}$����B��6��0������PΪ�߶�AB���е㣬���߶�AB�Ƶ�O��ʱ����ת90����P�Ķ�Ӧ��P��������ǣ�������| A�� | ��-3��$\sqrt{3}$�� | B�� | ��$-\sqrt{3}$��3�� | C�� | ��$\sqrt{3}$��-3�� | D�� | ��-1��$\sqrt{3}$�� |
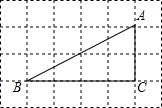 ��ͼ����ABC�Ķ��㶼�������������еĸ�㣬��cosA���ڣ�������
��ͼ����ABC�Ķ��㶼�������������еĸ�㣬��cosA���ڣ�������| A�� | $\frac{2\sqrt{5}}{5}$ | B�� | $\frac{\sqrt{5}}{5}$ | C�� | $\sqrt{5}$ | D�� | $\frac{2}{3}$ |
 ��ͼ��?ABCD�У�AD=3cm��AB=5cm��BD��AD����P�ӵ�A��������AD���������˶���ͬʱ��Q�ӵ�B��������BA���������˶��������˶����ٶ�Ϊ1cm/s�����˶���ʱ��Ϊx��s������CPQ�����Ϊy��cm2��������Q�˶�����Aʱ��P��Q��ֹͣ�˶���
��ͼ��?ABCD�У�AD=3cm��AB=5cm��BD��AD����P�ӵ�A��������AD���������˶���ͬʱ��Q�ӵ�B��������BA���������˶��������˶����ٶ�Ϊ1cm/s�����˶���ʱ��Ϊx��s������CPQ�����Ϊy��cm2��������Q�˶�����Aʱ��P��Q��ֹͣ�˶���