题目内容
7.函数y=$\frac{{x}^{2}+1}{|x|}$的大致图象是( )| A. | 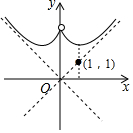 | B. | 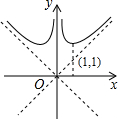 | C. |  | D. | 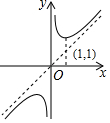 |
分析 本题可用排除法解答,根据y始终大于0,可排除D,再根据x的绝对值越接近于0(如x=±0.1,或x=±0.01)时,每个图象两侧都是无限上升,可排除A,根据函数y=$\frac{{x}^{2}+1}{|x|}$和y=$\frac{3}{2}$x有交点即可排除C,即可解题.
解答 解:x取±1,±2,±3,会发现最小值是x取±1时y=2,由此选项C,D错误;
x的绝对值越接近于0(如x=±0.1,或x=±0.01)时,每个图象两侧都是无限上升,可排除A,
∵当直线经过(0,0)和(1,1)时,直线解析式为y=x,
当y=x=$\frac{{x}^{2}+1}{|x|}$时,x无解,
∴y=x与y=$\frac{{x}^{2}+1}{|x|}$没有有交点,∴B正确;
故选B.
点评 此题主要考查了函数图象的性质,考查了平方根和绝对值大于等于0的性质,本题中求得直线与函数的交点是解题的关键.

练习册系列答案
相关题目
17.某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
得出结论:a.估计乙部门生产技能优秀的员工人数为240;b.可以推断出甲或乙部门员工的生产技能水平较高,理由为①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高..(至少从两个不同的角度说明推断的合理性)
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
| 成绩x 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 | 1 | 0 | 0 | 7 | 10 | 2 |
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
| 部门 | 平均数 | 中位数 | 众数 |
| 甲 | 78.3 | 77.5 | 75 |
| 乙 | 78 | 80.5 | 81 |
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高..(至少从两个不同的角度说明推断的合理性)
 如图,∠MON及ON上一点A.
如图,∠MON及ON上一点A.

 “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:
“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题: 如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.
如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$. 如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE:∠EFB=3:4,∠ABF=40°,那么∠BEF的度数为60°.
如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE:∠EFB=3:4,∠ABF=40°,那么∠BEF的度数为60°.