题目内容
2.“鸡兔同笼”是我国古代著名的数学趣题之一.大约在1500年前成书的《孙子算经》中,就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有35个头;从下面数,有94条腿.问笼中各有几只鸡和兔?分析 本题可设鸡有x只,兔有y只,因“今有雉(鸡)兔同笼,上有三十五头,下有九十四足.”,所以有$\left\{\begin{array}{l}{x+y=35}\\{2x+4y=94}\end{array}\right.$,解之得鸡的只数,兔的只数.
解答 解:设鸡有x只,兔有y只,根据题意得
有$\left\{\begin{array}{l}{x+y=35}\\{2x+4y=94}\end{array}\right.$,
解之,得$\left\{\begin{array}{l}{x=23}\\{y=12}\end{array}\right.$,
即有鸡23只,兔12只.
点评 本题考查了二元一次方程组的应用.注意:每只兔子有4只足,每只鸡有2只足.解题关键是弄清题意,合适的等量关系,列出方程组.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
12.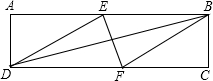 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
(1)若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$
(2)若DE2=BD•EF,则DF=2AD
那么,下面判断正确的是( )
 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:(1)若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$
(2)若DE2=BD•EF,则DF=2AD
那么,下面判断正确的是( )
| A. | ①正确,②正确 | B. | ①正确,②错误 | C. | ①错误,②正确 | D. | ①错误,②错误 |
17.某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号中选择:
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
| 污水处理器型号 | A型 | B型 |
| 处理污水能力(吨/月) | 240 | 180 |
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
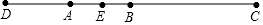 已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.
已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.

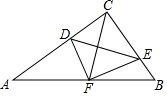 如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$.
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$. 在如图所示的两处各留1m宽的门,其余部分(不包括门)用篱笆围成.已知可用篱笆总长为18m,则能建成的矩形菜园占地面积最大为50m2.
在如图所示的两处各留1m宽的门,其余部分(不包括门)用篱笆围成.已知可用篱笆总长为18m,则能建成的矩形菜园占地面积最大为50m2.