题目内容
18.如图,某日的钱塘江观测信息如下: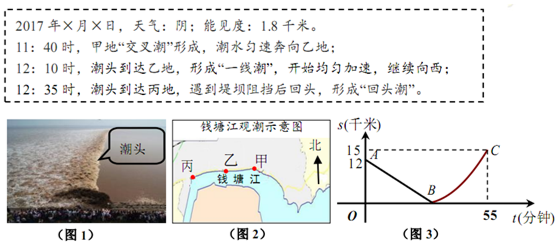
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示.其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数:s=$\frac{1}{125}$t2+bt+c(b,c是常数)刻画.
(1)求m值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+$\frac{2}{125}$(t-30),v0是加速前的速度).
分析 (1)根据起始时间结合到达乙地时间,即可求出m值,再根据速度=路程÷时间,即可求出潮头从甲地到乙地的速度;
(2)根据小红出发时间结合路程=速度×时间,可求出此时潮头离乙地的距离,再根据时间=路程÷二者速度和即可求出小红需多长时间与潮头相遇;
(3)根据点B、C的坐标利用待定系数法可求出二次函数解析式,令潮头的速度=小红的最高速度,可求出小红开始落后的时间,利用二次函数图象上点的坐标特征可求出此时潮头离开乙地的距离,再根据潮头离乙地的距离-小红离乙地的距离=1.8千米,即可求出t值,用其减去30加上潮头走完二者相遇到乙地的时间即可得出结论.
解答 解:(1)12时10分-11时40分=30分,
12÷30=0.4(千米/分).
答:m的值为30,
∴m的值为30.潮头从甲地到乙地的速度为0.4千米/分.
(2)0.4×(30+40-59)=4.4(千米),
4.4÷(0.4+0.48)=5(分钟).
答:小红出发五分钟后与潮头相遇.
(3)将B(30,0)、C(55,15)代入s=$\frac{1}{125}$t2+bt+c中,
得:$\left\{\begin{array}{l}{\frac{1}{125}×3{0}^{2}+30b+c=0}\\{\frac{1}{125}×5{5}^{2}+55b+c=15}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=-\frac{2}{25}}\\{c=-\frac{24}{5}}\end{array}\right.$,
∴曲线BC的函数关系式为s=$\frac{1}{125}$t2-$\frac{2}{25}$t-$\frac{24}{5}$.
令0.4+$\frac{2}{125}$(t-30)=0.48,解得:t=35,
当t=35时,s=$\frac{1}{125}$t2-$\frac{2}{25}$t-$\frac{24}{5}$=2.2.
根据题意得:$\frac{1}{125}$t2-$\frac{2}{25}$t-$\frac{24}{5}$-0.48(t-35)-2.2=1.8,
整理得:t2-70t+1000=0,
解得:t=50或t=20(不合题意,舍去).
∵0.48×5÷0.4=6(分钟),
∴50-30+6=26(分钟),
∴小红与潮头相遇到落后潮头1.8千米共需26分钟.
点评 本题考查了二次函数的应用、待定系数法求二次函数解析式、二次函数图象上点的坐标特征以及解一元二次方程,解题的关键是:(1)根据数量关系,列式计算;(2)求出小红出发时潮头离乙地的距离;(3)根据二者相距1.8千米,列出关于t的一元二次方程.

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 8 |
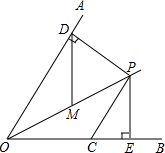 如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$.
如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$. 如图,⊙O的弦AB、CD交于点E,点A是$\widehat{CD}$的中点,连接AC、BC,延长DC到点P,连接PB.
如图,⊙O的弦AB、CD交于点E,点A是$\widehat{CD}$的中点,连接AC、BC,延长DC到点P,连接PB.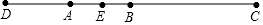 已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.
已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.