题目内容
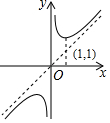
19. 如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.
如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.
分析 作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,则AG⊥BC,先求得△AOE≌△BAG,得出AG=OE=n,BG=AE=1,从而求得B(n+1,1-n),根据k=n×1=(n+1)(1-n)得出方程,解方程即可.
解答 解:作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,如图所示: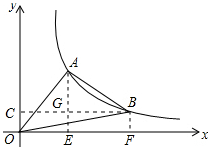
则AG⊥BC,
∵∠OAB=90°,
∴∠OAE+∠BAG=90°,
∵∠OAE+∠AOE=90°,
∴∠AOE=∠GAB,
在△AOE和△BAG中,$\left\{\begin{array}{l}{∠AOE=∠GAB}&{\;}\\{∠AOE=∠AGB=90°}&{\;}\\{AO=AB}&{\;}\end{array}\right.$,
∴△AOE≌△BAG(AAS),
∴OE=AG,AE=BG,
∵点A(n,1),
∴AG=OE=n,BG=AE=1,
∴B(n+1,1-n),
∴k=n×1=(n+1)(1-n),
整理得:n2+n-1=0,
解得:n=$\frac{-1\sqrt{5}}{2}$(负值舍去),
∴n=$\frac{\sqrt{5}-1}{2}$,
∴k=$\frac{\sqrt{5}-1}{2}$;
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识;熟练掌握反比例函数图象上点的坐标特征,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
8.一次函数y=-2x+m的图象经过点P(-2,3),且与x轴、y轴分别交于点A、B,则△AOB的面积是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 8 |
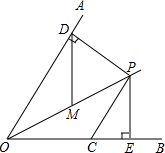 如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$.
如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$.

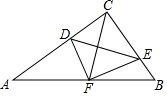 如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$.
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$. 荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:
荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为: 在如图所示的两处各留1m宽的门,其余部分(不包括门)用篱笆围成.已知可用篱笆总长为18m,则能建成的矩形菜园占地面积最大为50m2.
在如图所示的两处各留1m宽的门,其余部分(不包括门)用篱笆围成.已知可用篱笆总长为18m,则能建成的矩形菜园占地面积最大为50m2.