题目内容
17.某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
| 成绩x 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 | 1 | 0 | 0 | 7 | 10 | 2 |
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
| 部门 | 平均数 | 中位数 | 众数 |
| 甲 | 78.3 | 77.5 | 75 |
| 乙 | 78 | 80.5 | 81 |
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高..(至少从两个不同的角度说明推断的合理性)
分析 根据收集数据填写表格即可求解;
用乙部门优秀员工人数除以20乘以400即可得出答案,根据情况进行讨论分析,理由合理即可.
解答 解:填表如下:
| 成绩x 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 | 1 | 0 | 0 | 7 | 10 | 2 |
故估计乙部门生产技能优秀的员工人数为240;
b.答案不唯一,理由合理即可.
可以推断出甲部门员工的生产技能水平较高,理由为:
①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或可以推断出乙部门员工的生产技能水平较高,理由为:
①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.
故答案为:1,0,0,7,10,2;
240;甲或乙,①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高;
或①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.
点评 本题考查了众数、中位数以及平均数,掌握众数、中位数以及平均数的定义以及用样本估计总体是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.一次函数y=-2x+m的图象经过点P(-2,3),且与x轴、y轴分别交于点A、B,则△AOB的面积是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 8 |
5.一艘轮船在静水中的最大航速为35km/h,它以最大航速沿江顺流航行120km所用时间,与以最大航速逆流航行90km所用时间相等.设江水的流速为v km/h,则可列方程为( )
| A. | $\frac{120}{v+35}$=$\frac{90}{v-35}$ | B. | $\frac{120}{35-v}$=$\frac{90}{35+v}$ | C. | $\frac{120}{v-35}$=$\frac{90}{v+35}$ | D. | $\frac{120}{35+v}$=$\frac{90}{35-v}$ |
2.已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )
| A. | ∠BAC=∠DCA | B. | ∠BAC=∠DAC | C. | ∠BAC=∠ABD | D. | ∠BAC=∠ADB |

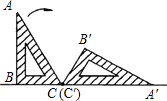 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为16πcm.
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为16πcm.