题目内容
2.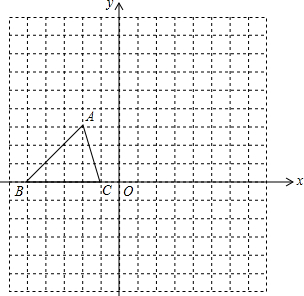 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).(1)画出点B关于点A的对称点B1,并写出点B1的坐标;
(2)画出△ABC绕点C逆时针旋转90°后的图形△A′B′C,并写出点B的对应点B′的坐标.
分析 (1)关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分,据此进行作图即可;
(2)根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
解答 解:(1)画出图形如图,点B1即为所求.
由图可得,点B1的坐标为(1,6);
(2)画出图形如图,△A'B'C即为所求,
由图可得,点B'的坐标为(-1,-4).
点评 本题主要考查了中心对称以及利用旋转变换进行作图,解决问题的关键是掌握中心对称以及旋转的概念,解题时注意:在旋转中,对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
17.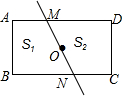 如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )
如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )
 如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )
如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )| A. | S1<S2 | B. | S1>S2 | ||
| C. | S1=S2 | D. | S1与S2的关系由直线的位置而定 |
7.下列运算正确的是( )
| A. | -a2•(-a3)=a6 | B. | (a2)-3=a-6 | C. | ($\frac{1}{a+1}$)-2=-a2-2a-1 | D. | (2a+1)0=1 |
14.抛物线y=3x2,y=-3x2,y=-3x2+3共有的性质是( )
| A. | 开口向上 | B. | 对称轴是y轴 | ||
| C. | 都有最高点 | D. | y随x值的增大而增大 |