题目内容
15．在?ABCD中，M，N分别是DC，AB的中点，若∠A=60°，AB=2AD，求证：MN⊥BD．分析 利用平行四边形的性质以及其判定方法得出四边形ANMD是平行四边形，再求出△ADN是等边三角形，进而得出答案．
解答 
证明：连接DN，
∵在?ABCD中，M，N分别是DC，AB的中点，
∴DM=AN，DM∥AN，
∴四边形ANMD是平行四边形，
∴AD∥MN，
∵AN=BN，AB=2AD，∠A=60°，
∴△ADN是等边三角形，
∴DN=AN=BN，
∴△ADB是直角三角形，
∴MN⊥BD．
点评 此题主要考查了平行四边形的判定与性质以及等边三角形的判定与性质，得出△ADN是等边三角形是解题关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
5．下列说法正确的是（ ）
| A． | 若$\frac{\sqrt{x-1}}{x-2}$有意义，则有x≥1且x≠2 | B． | 勾股定理是a2+b2=c2 | ||
| C． | 夹在两条平行线间的线段相等 | D． | a0=1 |
6．如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（ ）
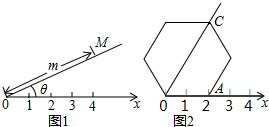
| A． | （60°，4） | B． | （45°，4） | C． | （60°，2） | D． | （50°，2） |
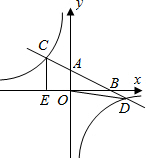如图在平面直角坐标系xOy中，直线y1=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A，与反比例函数y2=$\frac{k}{x}$（k≠0）的图象分别交于点C、D，CE⊥x轴于点E，OE=2．
7．已知点A（2，-3），线段AB与坐标轴平行，则点B的坐标可能是（ ）
| A． | （-1，-2） | B． | （3，-2） | C． | （1，2） | D． | （-2，-3） |
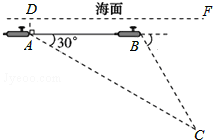如图，一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子，继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为55°．