题目内容
5.下列说法正确的是( )| A. | 若$\frac{\sqrt{x-1}}{x-2}$有意义,则有x≥1且x≠2 | B. | 勾股定理是a2+b2=c2 | ||
| C. | 夹在两条平行线间的线段相等 | D. | a0=1 |
分析 根据被开方数大于等于0,分母不等于0列式计算;勾股定理,两平行线间的距离的定义,以及零指数幂的定义对各选项分析判断利用排除法求解.
解答 解:A、由题意得,x-1≥0且x-2≠0,
解得x≥1且x≠2,故本选项正确;
B、应为勾股定理是a2+b2=c2,(a、b是直角边,c是斜边),故本选项错误;
C、应为夹在两条平行线间的平行线段相等,故本选项错误;
D、a0=1(a≠0),故本选项错误.
故选A.
点评 本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.

练习册系列答案
相关题目
15.设[x]表示不大于x的最大整数,则对任意实数x,y,下列说法:①[-x]=-[x];②[2x]=2[x];③若|x-y|<1,则[x]=[y];④若x-y>1,则[x]-[y]≥1;⑤[x-y]≤[x]-[y],正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.某校有A,B两个电脑教室,甲,乙,丙三名学生各自随机选择其中的一个电脑教室上课.求甲,乙,丙三名学生在同一个电脑教室上课的概率( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
17.饭店为某公司提供“白领午餐”,有12元、15元、18元三种价格的套餐可供选择,每人限购一份.本周销售套餐共计500份,其中12元的占总份数的20%,15元的卖出180份,其余均为18元的,那么所购买的盒饭费用的中位数和众数分别是( )
| A. | 15元和18元 | B. | 15元和15元 | C. | 18元和15元 | D. | 18元和18元 |
14.化简$\frac{{a}^{2}}{a-b}$-$\frac{{b}^{2}}{a-b}$的结果是( )
| A. | a+b | B. | a | C. | a-b | D. | b |
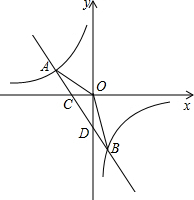 一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).