题目内容
11.已知关于x的二次函数y=x2+(k2-3k-4)x+2k的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.(1)求k的值;
(2)在(1)的条件下,若反比例函数y=$\frac{m}{x}$的图象与二次函数y=x2+(k2-3k-4)x+2k的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(xR,yR),S(xs,ys)中的纵坐标yR,ys分别是一元二次方程y2+my-1=0的解,求四边形AQBS的面积S四边形AQBS;
(3)在(1),(2)的条件下,在x轴下方是否存在二次函数y=x2+(k2-3k-4)x+2k图象上的点P使得S△PAB=2S△RAB?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)设A点坐标为(x1,0),B点坐标为(x2,0),由A、B两点关于原点对称,即可得x1+x2=0,又由x1+x2=-(k2-3k-4),即可求得k的值;
(2)由Q点的坐标求出m的值,从而确定一元二次方程y2-my-1=0即为y2+y-1=0,解得:y=$\frac{-1±\sqrt{5}}{2}$,因为点R在点S的左边,所以${y}_{R}=\frac{-1-\sqrt{5}}{2},{y}_{S}=\frac{-1+\sqrt{5}}{2}$,由(1)得二次函数y=x2-2,令x2-2=0,解得:${x}_{1}=-\sqrt{2},{x}_{2}=\sqrt{2}$,所以A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),即可求得AB的长,又由四边形AQBS的面积为:S△AQB+S△ASB求得答案;
(3)由抛物线的顶点坐标为(0,-2),假设满足条件的点P存在,由S△PAB=2S△RAB,可得点P的纵坐标,即可得即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB.
解答 解:(1)设A点坐标为(x1,0),B点坐标为(x2,0),
∵A、B两点关于原点对称,
∴x1+x2=0,
又x1+x2=-(k2-3k-4),
则k2-3k-4=0,
解得k1=-1,k2=4,
当k=4时,抛物线为y=x2+8,此时△=-32<0,舍去;
当k=-1时,抛物线为y=x2-2,此时△=8>0,则抛物线与x轴交于两点,
故所求k值为-1.
(2)如图: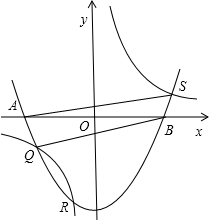
∵Q的坐标为(-1,-1),在y=$\frac{m}{x}$上,
∴$-1=\frac{m}{-1}$,
解得:m=1,
∴一元二次方程y2-my-1=0即为y2+y-1=0,
解得:y=$\frac{-1±\sqrt{5}}{2}$,
∵点R在点S的左边,
∴${y}_{R}=\frac{-1-\sqrt{5}}{2},{y}_{S}=\frac{-1+\sqrt{5}}{2}$,
由(1)得二次函数y=x2-2,令x2-2=0,解得:${x}_{1}=-\sqrt{2},{x}_{2}=\sqrt{2}$,
∴A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),
∴AB=|$\sqrt{2}-(-\sqrt{2})$|=2$\sqrt{2}$,
则四边形AQBS的面积为:${S}_{△AQB}+{S}_{△ABS}=\frac{1}{2}AB•|{y}_{Q}|+\frac{1}{2}AB•$|yS|=$\frac{1}{2}×2\sqrt{2}×1+\frac{1}{2}×2\sqrt{2}×\frac{-1+\sqrt{5}}{2}=\frac{\sqrt{10}+\sqrt{2}}{2}$.
(3)∵抛物线的顶点坐标为(0,-2),假设满足条件的点P存在,
则∵S△PAB=2S△RAB,
∴点P的纵坐标为:2×($\frac{-1-\sqrt{5}}{2}$)=-1$-\sqrt{5}$,
而-1-$\sqrt{5}<-2$,
∴P点不存在.
即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB.
点评 此题考查了二次函数与一元二次方程的关系,点与函数的关系以及四边形的面积求解方法等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.

| A. | x≥-2 | B. | x≤1 | C. | -2≤x≤1 | D. | 无解 |
| A. | 1000 | B. | 1100 | C. | 1200 | D. | 1300 |
| A. | y=x+3 | B. | y=x-3 | C. | y=-x+1 | D. | y=-x-1 |
| 身高(cm) | 165 | 168 | 170 | 171 | 172 |
| 人数(名) | 4 | 6 | 5 | 3 | 2 |
| A. | 169cm,169cm | B. | 168cm,168cm | C. | 172cm,169cm | D. | 168cm,169cm |
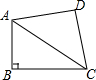 如图,∠ABC=90°,AB=6,BC=8,AD=CD=7,若点P到AC的距离为5,则点P在四边形ABCD边上的个数为( )
如图,∠ABC=90°,AB=6,BC=8,AD=CD=7,若点P到AC的距离为5,则点P在四边形ABCD边上的个数为( )