题目内容

16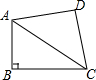．如图，∠ABC=90°，AB=6，BC=8，AD=CD=7，若点P到AC的距离为5，则点P在四边形ABCD边上的个数为（　　）
A．0B．2C．3D．4

分析 作DE⊥AC，垂足为E；BF⊥AC，垂足为F．求出DE、BF的长，与5比较大小即可作出判断．

解答 解：作DE⊥AC，垂足为E；BF⊥AC，垂足为F．
在△ACD中，AE=CE=5，
DE=$\sqrt{{7}^{2}-{5}^{2}}$=2$\sqrt{6}$，5；
在△ABC中，BF=$\frac{6×8}{10}$=4.8＜5，
点P到AC的距离为5，则点P在四边形ABCD边上的个数为0．
故选A．

点评 本题考查了勾股定理、点到直线的距离，找到直角三角形是解题的关键．

练习册系列答案
相关题目
6．解二元一次方程组：$\left\{\begin{array}{l}{x+y=5}\\{2x-y=4}\end{array}\right.$．
7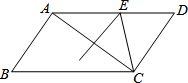．如图，在平行四边形ABCD中，AB=8，BC=12，AC的垂直平分线交AD于点E，则△CDE的周长是（　　）
A．14B．20C．22D．24
4．为了解中考体育科目训练情况，改进训练方法，减轻学生负担，某县教育局从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如图两幅不完整的统计图．
请根据统计图中的信息解答下列问题：
（1）本次抽样测试的学生人数是40；
（2）图中∠α的度数是54°，并把图2条形统计图补充完整；
（3）全县九年级共有学生8500名，如果全部参加这次中考体育科目测试，请估计不及格的人数为1700．
11．已知关于x的二次函数y=x2+（k2-3k-4）x+2k的图象与x轴从左到右交于A，B两点，且这两点关于原点对称．
（1）求k的值；
（2）在（1）的条件下，若反比例函数y=$\frac{m}{x}$的图象与二次函数y=x2+（k2-3k-4）x+2k的图象从左到右交于Q，R，S三点，且点Q的坐标为（-1，-1），点R（xR，yR），S（xs，ys）中的纵坐标yR，ys分别是一元二次方程y2+my-1=0的解，求四边形AQBS的面积S四边形AQBS；
（3）在（1），（2）的条件下，在x轴下方是否存在二次函数y=x2+（k2-3k-4）x+2k图象上的点P使得S△PAB=2S△RAB？若存在，求出点P的坐标；若不存在，请说明理由．
1．二元一次方程组$\left\{\begin{array}{l}{x+2y=3}\\{2x-y=1}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$．
8．菱形ABCD中，对角线AC，BD交于点O，BE⊥AD交AC于F，AF=BD，G为BD上的点，EG∥AB．
（1）求证：△AEF≌△BED；
（2）求证：BO=（$\sqrt{2}$+1）OG．
5．小明在学习反比例函数的图象时，他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤，在纸上逐步探索函数y2=$\frac{2}{x}$的图象，并且在黑板上写出4个点的坐标：A$（\;\frac{3}{2}，\frac{4}{3}\;）$，B（1，2），C$（\;1，\;\frac{1}{2}\;）$，D（-2，-1）．
（1）在A、B、C、D四个点中，任取一个点，这个点既在直线y1=x+1又在双曲线y2=$\frac{2}{x}$上的概率是多少？
（2）小明从A、B、C、D四个点中任取两个点进行描点，求两点都落在双曲线y2=$\frac{2}{x}$上的概率．
6．-4的相反数是（　　）
A．4B．-$\frac{1}{4}$C．$\frac{1}{4}$D．-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网