题目内容
19.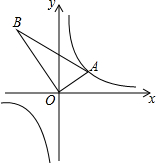 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
分析 要求函数的解析式只要求出B点的坐标就可以,过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.根据条件得到△ACO∽△ODB,得到:$\frac{BD}{OC}$=$\frac{OD}{AC}$=$\frac{OB}{OA}$=2,然后用待定系数法即可.
解答  解:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
解:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA,
∴$\frac{BD}{OC}$=$\frac{OD}{AC}$=$\frac{OB}{OA}$,
∵OB=2OA,
∴BD=2m,OD=2n,
因为点A在反比例函数y=$\frac{1}{x}$的图象上,则mn=1,
∵点B在反比例函数y=$\frac{k}{x}$的图象上,B点的坐标是(-2n,2m),
∴k=-2n•2m=-4mn=-4.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征,相似三角形的判定和性质,求函数的解析式的问题,一般要转化为求点的坐标的问题,求出图象上点的横纵坐标的积就可以求出反比例函数的解析式.

练习册系列答案
相关题目
7.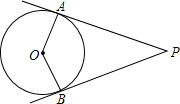 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )| A. | 150° | B. | 130° | C. | 155° | D. | 135° |
14.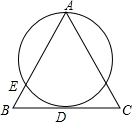 如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
 如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )| A. | 线段AE的中垂线与线段AC的中垂线的交点 | |
| B. | 线段AB的中垂线与线段AC的中垂线的交点 | |
| C. | 线段AE的中垂线与线段BC的中垂线的交点 | |
| D. | 线段AB的中垂线与线段BC的中垂线的交点 |
11.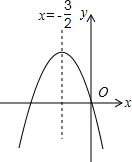 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.若代数式$\frac{1}{x-1}$+$\sqrt{x}$有意义,则实数x的取值范围是( )
| A. | x≠1 | B. | x≥0 | C. | x≠0 | D. | x≥0且x≠1 |
 如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是(400,800).
如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是(400,800).