若关于x.y的二元一次方程组$\left\{\begin{array}{l}{2x-y=-1-a}\\{x-2y=3}\end{array}\right.$的解满足x+y＞-2.则a的取值范围是( )A．a＜-2B．a＞2C．a＜2D．a＞-2 题目和参考答案——青夏教育精英家教网—

题目内容

2．若关于x，y的二元一次方程组$\left\{\begin{array}{l}{2x-y=-1-a}\\{x-2y=3}\end{array}\right.$的解满足x+y＞-2，则a的取值范围是（　　）

A．

a＜-2

B．

a＞2

C．

a＜2

D．

a＞-2

分析方程组中两方程相减表示出x+y，代入已知不等式即可求出a的范围．

解答解：$\left\{\begin{array}{l}{2x-y=-1-a①}\\{x-2y=3②}\end{array}\right.$，
①-②得：x+y=-4-a，
代入不等式得：-4-a＞-2，
解得：a＜-2，
故选A．

点评此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．

练习册系列答案

相关题目

7．若α为锐角，则sinα+cosα的值（　　）

13．若x₁，x₂，x₃，x₄，x₅满足方程组：$\left\{\begin{array}{l}2{x_1}+{x_2}+{x_3}+{x_4}+{x_5}=6\\{x_1}+2{x_2}+{x_3}+{x_4}+{x_5}=12\\{x_1}+{x_2}+2{x_3}+{x_4}+{x_5}=24\\{x_1}+{x_2}+{x_3}+2{x_4}+{x_5}=48\\{x_1}+{x_2}+{x_3}+{x_4}+2{x_5}=96\end{array}\right.$；则3x₄+2x₅的值是181．

10．若实数a，b（a≠b）分别满足方程a²-7a+2=0，b²-7b+2=0，则$\frac{b}{a}$$+\frac{a}{b}$的值为（　　）

年份x	1960	1974	1987	1999	2010
人口数y/亿	30	40	50	60	69

（1）根据表中的数据，在直角坐标系中画出世界人口增长曲线图；
（2）选择一个近似于人口增长曲线的一次函数，写出它的解析式；
（3）按照这样的增长趋势，估计2020年的世界人口数．

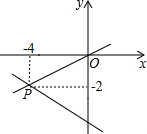7．写一个解为$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$的方程组：$\left\{\begin{array}{l}{x+y=-1}\\{x-y=3}\end{array}\right.$（写一个即可）．

14．

如图，已知y=ax+b和y=kx的图象交于点P，根据图象可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$．

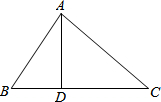11．使等式$\sqrt{\frac{3a-1}{a-2}}$=$\frac{\sqrt{3a-1}}{\sqrt{a-2}}$成立的实数a的取值范围是a＞2．

12．

如图，在△ABC中，D是BC边上一点，AB=13，AD=12，BD=5，CD=9，求AC的长．

试题分类