题目内容
17.世界人口统计表| 年份x | 1960 | 1974 | 1987 | 1999 | 2010 |
| 人口数y/亿 | 30 | 40 | 50 | 60 | 69 |
(2)选择一个近似于人口增长曲线的一次函数,写出它的解析式;
(3)按照这样的增长趋势,估计2020年的世界人口数.
分析 (1)根据表格中的数对建立平面直角坐标系描点连线即可;
(2)设直线解析式为y=kx+b,代入表格中(1999,60),(2010,69)即可求出解析式;
(3)把y=2020代入函数表达式求出x的值即可.
解答 解:(1)①绘出横坐标轴,逐段标上年份;②绘出纵坐标轴,标上人口数目;③将表中各年的人口数据用点标注出来,再用平滑的线连接起来,完成人口增长曲线图;
(2)设人口增长的一次函数的解析式为:y=kx+b,
代入(1999,60),(2010,69)得:$\left\{\begin{array}{l}{1999k+b=60}\\{2010k+b=69}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{9}{11}}\\{b=-1575}\end{array}\right.$,
∴y=$\frac{9}{11}$x-1575;
(3)把x=2020代入y=$\frac{9}{11}$x-1575,
则y=77.
点评 本题考查了一次函数的应用,选取与2020年靠近的两个点用待定系数法求出一次函数表达式.

练习册系列答案
相关题目
8.化简$\frac{{\sqrt{2}+\sqrt{5}-\sqrt{3}}}{{2\sqrt{30}-6\sqrt{2}+4\sqrt{3}}}$的结果是( )
| A. | $2\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{12}$ |
5.若式子$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≥0 |
2.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y=-1-a}\\{x-2y=3}\end{array}\right.$的解满足x+y>-2,则a的取值范围是( )
| A. | a<-2 | B. | a>2 | C. | a<2 | D. | a>-2 |
9.某电脑公司有A,B,C三种型号的电脑,其相应的价格如表:
已知某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种不同型号的电脑.请设计出几种不同的购买方案供该校选择,并说明理由.
| 型号 | A | B | C |
| 单价(元/台) | 6000 | 4000 | 2500 |
7.函数y=$\sqrt{x-8}$中自变量x的取值范围是( )
| A. | x≥8 | B. | x>8 | C. | x≤-8 | D. | x≠-8 |
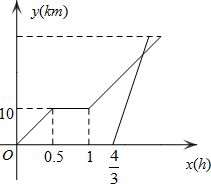 周末,小华骑自行车从家出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分后,爸爸开车沿相同路线前往植物园.如图是他们离家的路程y(km)y与小华离家的时间x(h)的函数图象,已知爸爸开车的速度是小华骑车速度的3倍.若爸爸比小华早10分达到植物园,则从小华家到植物园的路程是30km.
周末,小华骑自行车从家出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分后,爸爸开车沿相同路线前往植物园.如图是他们离家的路程y(km)y与小华离家的时间x(h)的函数图象,已知爸爸开车的速度是小华骑车速度的3倍.若爸爸比小华早10分达到植物园,则从小华家到植物园的路程是30km.