题目内容
13.若x1,x2,x3,x4,x5满足方程组:$\left\{\begin{array}{l}2{x_1}+{x_2}+{x_3}+{x_4}+{x_5}=6\\{x_1}+2{x_2}+{x_3}+{x_4}+{x_5}=12\\{x_1}+{x_2}+2{x_3}+{x_4}+{x_5}=24\\{x_1}+{x_2}+{x_3}+2{x_4}+{x_5}=48\\{x_1}+{x_2}+{x_3}+{x_4}+2{x_5}=96\end{array}\right.$;则3x4+2x5的值是181.分析 本题的方程组为对称轮换式,把5个方程相加得x1+x2+x3+x4+x5=31,要求x4、x5,就分别与④⑤相减即可.
解答 解:①+②+③+④+⑤得6x1+6x2+6x3+6x4+6x5=186
解得x1+x2+x3+x4+x5=31 ⑥
④-⑥得:x4=17,
⑤-⑥得:x5=65,
∴3x4+2x5=3×17+2×65=181.
故答案为:181.
点评 本题考查了代数式的求值,代数式中涉及的字母为方程组的未知数,虽然方程组比较复杂,但有一定的规律,需要观察规律求解.

练习册系列答案
相关题目
18.计算:-3+4的结果等于( )
| A. | 7 | B. | -7 | C. | 1 | D. | -1 |
8.化简$\frac{{\sqrt{2}+\sqrt{5}-\sqrt{3}}}{{2\sqrt{30}-6\sqrt{2}+4\sqrt{3}}}$的结果是( )
| A. | $2\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{12}$ |
18.某校八年级五班有7个合作学习小组,各学习小组的人数分别为:5,5,6,x,7,7,6,已知这组数据的平均数是6,则这组数据的众数和中位数分别是( )
| A. | 7,6 | B. | 6,6 | C. | 5,5 | D. | 7,7 |
5.若式子$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≥0 |
2.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y=-1-a}\\{x-2y=3}\end{array}\right.$的解满足x+y>-2,则a的取值范围是( )
| A. | a<-2 | B. | a>2 | C. | a<2 | D. | a>-2 |
3.下列调查,适合用全面调查的是( )
| A. | 了解一批炮弹的杀伤半径 | |
| B. | 了解某电视台《我是大明星》栏目的收视率 | |
| C. | 对市场上某种酒质量情况的调查 | |
| D. | 调查一架隐形战机的各零部件的质量 |
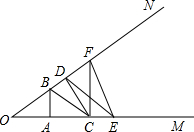 如图,∠MON两边上分别有A,C,E及D,F,B六个点,且S△OAB=S△ABC=S△BCD=S△CDE=S△DEF=1,则S△CDF=$\frac{3}{4}$.
如图,∠MON两边上分别有A,C,E及D,F,B六个点,且S△OAB=S△ABC=S△BCD=S△CDE=S△DEF=1,则S△CDF=$\frac{3}{4}$.