题目内容
5.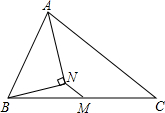 如图,△ABC中,已知M是BC边的中点,AN平分∠BAC,BN⊥AN,若AB=8cm,AC=16cm,则MN=4cm.
如图,△ABC中,已知M是BC边的中点,AN平分∠BAC,BN⊥AN,若AB=8cm,AC=16cm,则MN=4cm.
分析 延长BN交AC于D,根据等腰三角形的性质得到AD=AB=8cm,BN=ND,根据三角形中位线定理得到MN=$\frac{1}{2}$DC,得到答案.
解答 解: 延长BN交AC于D,
延长BN交AC于D,
∵AN平分∠BAC,BN⊥AN,
∴AD=AB=8cm,BN=ND,
∴DC=AC-AD=8cm,
∵M是BC边的中点,BN=ND,
∴MN=$\frac{1}{2}$DC=4cm,
故答案为:4.
点评 本题考查的是三角形中位线定理和等腰三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半以及等腰三角形的三线合一是解题的关键.

练习册系列答案
相关题目
17. 如图,△ABC≌△DEF,则下列判断错误的是( )
如图,△ABC≌△DEF,则下列判断错误的是( )
 如图,△ABC≌△DEF,则下列判断错误的是( )
如图,△ABC≌△DEF,则下列判断错误的是( )| A. | AB=DE | B. | BE=CF | C. | AC∥DF | D. | ∠ACB=∠DEF |
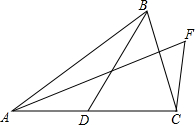 如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF.
如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF.