题目内容
 如图,在△AOB中,∠AOB=90°,AO=3,BO=6,将△AOB绕顶点O逆时针旋转到△A′OB′的位置.若此时线段A′B′与BO的交点C是BO的中点,则线段B′C的长度为
如图,在△AOB中,∠AOB=90°,AO=3,BO=6,将△AOB绕顶点O逆时针旋转到△A′OB′的位置.若此时线段A′B′与BO的交点C是BO的中点,则线段B′C的长度为考点:旋转的性质
专题:
分析:如图,作辅助线;首先求出AB、cos∠A的值;然后证明cos∠A′=cos∠A,A′M=CM;求出A′M的值,即可解决问题.
解答: 解:如图,过点O作OM⊥A′C;
解:如图,过点O作OM⊥A′C;
∵∠AOB=90°,AO=3,BO=6,
∴AB=
=3
,cos∠A=
=
;
由题意得:∠A′=∠A,OA′=OA=3,A′B′=AB=3
;
∵点C为BC的中点,
∴OC=
OB=3,OC=OA′,而OM⊥A′C,
∴A′M=CM;
∵cos∠A′=cos∠A,且cos∠A′=
,
∴A′M=
,B′C=3
-2×
=
故答案为
.
 解:如图,过点O作OM⊥A′C;
解:如图,过点O作OM⊥A′C;∵∠AOB=90°,AO=3,BO=6,
∴AB=
| 32+62 |
| 5 |
| 3 | ||
3
|
| ||
| 5 |
由题意得:∠A′=∠A,OA′=OA=3,A′B′=AB=3
| 5 |
∵点C为BC的中点,
∴OC=
| 1 |
| 2 |
∴A′M=CM;
∵cos∠A′=cos∠A,且cos∠A′=
| A′M |
| A′O |
∴A′M=
3
| ||
| 5 |
| 5 |
3
| ||
| 5 |
9
| ||
| 5 |
故答案为
9
| ||
| 5 |
点评:该题主要考查了旋转变换的性质、勾股定理、等腰三角形的性质等知识点及其应用问题;解题的关键是作辅助线,灵活运用旋转变换的性质、勾股定理等来分析、判断、解答.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=8,则PD=( )
如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=8,则PD=( )| A、3 | B、4 | C、5 | D、6 |
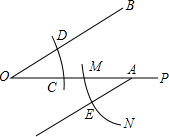 已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )
已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )| A、CD∥ME |
| B、OB∥AE |
| C、∠ODC=∠AEM |
| D、∠ACD=∠EAP |
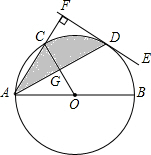 如图,⊙O的直径AB=10,C、D是圆上的两点,且
如图,⊙O的直径AB=10,C、D是圆上的两点,且
 如图,在△ABC中,D是AC的中点,过A、B、D三点的⊙O交BC于E且点D是弧
如图,在△ABC中,D是AC的中点,过A、B、D三点的⊙O交BC于E且点D是弧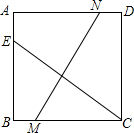 已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数.
已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数. 如图,在菱形ABCD中,BE⊥AD,BF⊥CD,E,F为垂足,
如图,在菱形ABCD中,BE⊥AD,BF⊥CD,E,F为垂足, 某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由.
某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由.