题目内容
 如图,四边形ABCD和四边形AEFG是正方形,△AED是等边三角形,则图中度数为30°的角有( )
如图,四边形ABCD和四边形AEFG是正方形,△AED是等边三角形,则图中度数为30°的角有( )| A、2个 | B、3个 | C、4个 | D、5个 |
考点:正方形的性质,等边三角形的性质
专题:
分析:由正方形的性质结合条件可求得∠BAE=∠EDC=30°,设BC交EF于点M,可求得∠BME=150°,可求得∠BMF=∠EMC=30°,可得出答案.
解答: 解:如图,设BC、EF交于点M,
解:如图,设BC、EF交于点M,
∵△AED为等边三角形,
∴∠EAD=∠EDA=60°,
又∵四边形ABCD为正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAE=∠EDC=30°,
∵四边形AEFG为正方形,
∴∠AEF=90°,
在四边形ABME中,
∵∠BAE+∠B+∠AEF+∠BME,
∴∠BME=150°,
∴∠BMF=∠EMC=30°,
∴度数为30°的角有4个,
故选C.
 解:如图,设BC、EF交于点M,
解:如图,设BC、EF交于点M,∵△AED为等边三角形,
∴∠EAD=∠EDA=60°,
又∵四边形ABCD为正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAE=∠EDC=30°,
∵四边形AEFG为正方形,
∴∠AEF=90°,
在四边形ABME中,
∵∠BAE+∠B+∠AEF+∠BME,
∴∠BME=150°,
∴∠BMF=∠EMC=30°,
∴度数为30°的角有4个,
故选C.
点评:本题主要考查正方形和等边三角形的性质,掌握正方形的四个角都是直角、等边三角形的每个角都是60°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
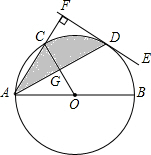 如图,⊙O的直径AB=10,C、D是圆上的两点,且
如图,⊙O的直径AB=10,C、D是圆上的两点,且
 如图,在△ABC中,D是AC的中点,过A、B、D三点的⊙O交BC于E且点D是弧
如图,在△ABC中,D是AC的中点,过A、B、D三点的⊙O交BC于E且点D是弧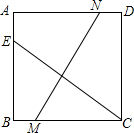 已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数.
已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数. 如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF.
如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF. 如图,在菱形ABCD中,BE⊥AD,BF⊥CD,E,F为垂足,
如图,在菱形ABCD中,BE⊥AD,BF⊥CD,E,F为垂足, 如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=3,AB=4,AD=12,在AD上能否找到一点P,使△PAB和△PCD相似?若能,共有几个符合条件的点P?并求相应PD的长.若不能,说明理由.
如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=3,AB=4,AD=12,在AD上能否找到一点P,使△PAB和△PCD相似?若能,共有几个符合条件的点P?并求相应PD的长.若不能,说明理由. 如图是某几何体的展开图
如图是某几何体的展开图