题目内容
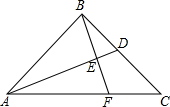 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D为BC边的中点,BE⊥AD于点E,交AC于点F,求
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D为BC边的中点,BE⊥AD于点E,交AC于点F,求| AF |
| FC |
考点:平行线分线段成比例
专题:
分析:如图,作辅助线;首先证明DE=DG;然后运用勾股定理、射影定理等求出AE、EG的长度;运用平行线分线段成比例定理证明
=
=
,即可解决问题.
| AF |
| FC |
| AE |
| EG |
| 2 |
| 1 |
解答: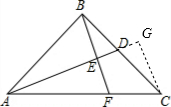 解:如图,过点C作CG⊥AD,交AD的延长线于点G;
解:如图,过点C作CG⊥AD,交AD的延长线于点G;
∵BE⊥AD,
∴BE∥CG,△BDE∽△CDG,
∴
=
,
∵BD=CD,
∴DE=DG;
设AB=2λ,则BD=λ;
∵∠ABD=90°,BE⊥AD,
∴AD=
=
λ,AB2=AE•AD,
∴AE=
λ,DE=AD-AE=
λ,
∴GE=2DE=
;
∵EF∥CG,
∴
=
=
.
 解:如图,过点C作CG⊥AD,交AD的延长线于点G;
解:如图,过点C作CG⊥AD,交AD的延长线于点G;∵BE⊥AD,
∴BE∥CG,△BDE∽△CDG,
∴
| BD |
| CD |
| DE |
| DG |
∵BD=CD,
∴DE=DG;
设AB=2λ,则BD=λ;
∵∠ABD=90°,BE⊥AD,
∴AD=
| 4λ2+λ2 |
| 5 |
∴AE=
4
| ||
| 5 |
| ||
| 5 |
∴GE=2DE=
2
| ||
| 5 |
∵EF∥CG,
∴
| AF |
| FC |
| AE |
| EG |
| 2 |
| 1 |
点评:该题主要考查了平行线分线段成比例定理及其应用问题;解题的关键是作辅助线,构造相似三角形,灵活运用平行线分线段成比例定理、相似三角形的判定及其性质等来分析、解答.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知方程组
的解为
,则a-b的值为( )
|
|
| A、10 | ||
B、
| ||
C、-
| ||
| D、-10 |
在2012年全国初中数学竞赛复赛中,成都市某校9年级10名参赛学生成绩分别为:84,85,86,84,86,87,87,86,87,87,则这组数据的中位数和众数分别是( )
| A、86;87 |
| B、87;86 |
| C、86.5;87 |
| D、87;86.5 |
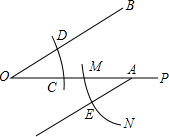 已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )
已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )| A、CD∥ME |
| B、OB∥AE |
| C、∠ODC=∠AEM |
| D、∠ACD=∠EAP |
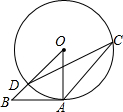 如图,AB与圆O相切于点A,且OA=AB,则∠DCA的度数是( )
如图,AB与圆O相切于点A,且OA=AB,则∠DCA的度数是( )| A、45° | B、30° |
| C、60° | D、22.5° |
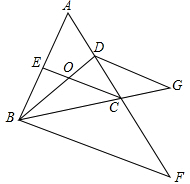 如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.
如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.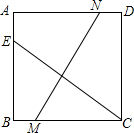 已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数.
已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数.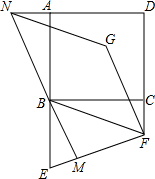 如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,连接BF、EF,恰有BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作EF的垂线,交EF于点M,交DA的延长线于点N,连接NG.
如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,连接BF、EF,恰有BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作EF的垂线,交EF于点M,交DA的延长线于点N,连接NG. 如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD?
如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD?