题目内容
19.(1)在?ABCD中,∠A=60°,AB=10,AD=12,求S?ABCD;(2)在?ABCD中,∠A=α(0°<α<90°),AB=x,AD=y,求S?ABCD.
分析 (1)过点D作DE⊥AB,根据直角三角形的性质,求得DE,再根据平行四边形的面积计算即可;
(2)过点D作DE⊥AB,解直角三角形得到DE,再根据平行四边形的面积计算即可.
解答 解:(1)过点D作DE⊥AB,垂足为E,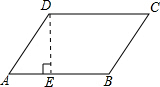
∴∠AED=90°,
∵∠A=60°,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD,
∵AD=12,
∴AE=6,
∴由勾股定理得DE=6$\sqrt{3}$,
∵AB=10,
∴S?ABCD=AB•DE=10×6$\sqrt{3}$=60$\sqrt{3}$;
(2)过点D作DE⊥AB,垂足为E,
∴∠AED=90°,
∵∠A=α,
∵AD=y,
∴DE=y•sinα,∵AB=x,
∴S?ABCD=AB•DE=xysinα.
点评 本题考查了平行四边形的性质,以及平行四边形的面积、直角三角形的性质,解题关键是求平行四边形的高.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
9.一元二次方程(x-2)(x+3)=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
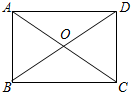 如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2cm,则AD的长为2$\sqrt{3}$cm.
如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2cm,则AD的长为2$\sqrt{3}$cm.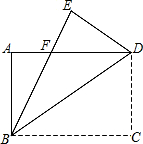 如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?
如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?