题目内容
7.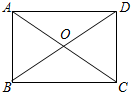 如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2cm,则AD的长为2$\sqrt{3}$cm.
如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2cm,则AD的长为2$\sqrt{3}$cm.
分析 矩形的对角线相等且互相平分,可得到△AOB是等边三角形,即可求得BD长,进而利用勾股定理可求得AD长.
解答 解:∵四边形ABCD为矩形.
∴OA=OB=OD=OC=2cm.
∴BD=OB+OD=2+2=4cm.
在直角三角形ABD中,AB=2,BD=4cm.
由勾股定理可知AD2=BD2-AB2=42-22=12cm.
∴AD=2$\sqrt{3}$cm.
故答案为2$\sqrt{3}$.
点评 本题考查矩形的性质及勾股定理的运用.用的知识点为:矩形的对角线相等且互相平分,熟记矩形的各种性质是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.若代数式5x2a-1y与-3x7y3a+b能合并成一项,则a+b=( )
| A. | -7 | B. | 15 | C. | 21 | D. | 8 |
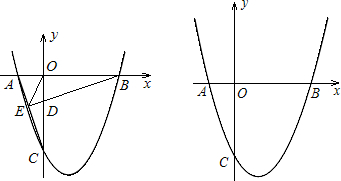
 已知:如图,BE⊥CD,BE=DE,BC=DA.
已知:如图,BE⊥CD,BE=DE,BC=DA.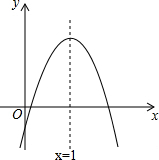 二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)
二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)