题目内容
8.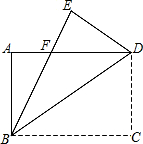 如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?
如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?
分析 由折叠的性质得到三角形BDC与三角形BDE全等,进而得到对应边相等,对应角相等,再由两直线平行内错角相等,等量代换及等角对等边得到FD=FB,设FD=FB=xcm,则AF=(8-x)cm,在直角三角形AFB中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出FD的长,进而求出三角形BDF面积.
解答 解:由折叠可得:△BDC≌△BDE,
∴∠CBD=∠EBD,BC=BE=8cm,ED=DC=AB=6cm,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠EBD,
∴FD=FB,
设FD=FB=xcm,则有AF=AD-FD=(8-x)cm,
在Rt△ABF中,根据勾股定理得:x2=(8-x)2+62,
解得:x=$\frac{25}{4}$,即FD=$\frac{25}{4}$cm,
则S△BDF=$\frac{1}{2}$FD•AB=$\frac{75}{4}$cm2.
点评 此题考查了翻折变换(折叠问题),涉及的知识有:折叠的性质,全等三角形的性质,平行线的性质,等腰三角形的判定,以及勾股定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 已知:如图,BE⊥CD,BE=DE,BC=DA.
已知:如图,BE⊥CD,BE=DE,BC=DA.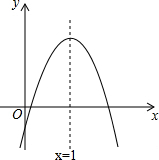 二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)
二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)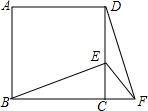 如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.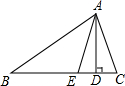 如图,在△ABC中,AD⊥BC于D,AE为∠BAC的平分线,且∠DAE=15°,∠B=35°,则∠C=65°.
如图,在△ABC中,AD⊥BC于D,AE为∠BAC的平分线,且∠DAE=15°,∠B=35°,则∠C=65°.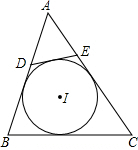 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9.
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9.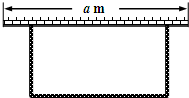 若用40m的篱笆围成一个一边靠墙的矩形场地,墙长a m,垂直于墙的边长为x m,围成的矩形场地的面积为y m2.
若用40m的篱笆围成一个一边靠墙的矩形场地,墙长a m,垂直于墙的边长为x m,围成的矩形场地的面积为y m2.