题目内容
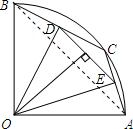 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为O,E.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为O,E.(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由.
(3)当OD=
| 3 |
考点:垂径定理,三角形中位线定理
专题:
分析:(1)证明BD=DC=0.5,借助勾股定理即可解决问题.
(2)证明DE为△ABC的中位线,求出AB的长度,即可解决问题.
(3)求出∠DOE=45°,此为解决问题的关键性结论;运用余弦定理列出关于线段OE的方程即可解决问题.
(2)证明DE为△ABC的中位线,求出AB的长度,即可解决问题.
(3)求出∠DOE=45°,此为解决问题的关键性结论;运用余弦定理列出关于线段OE的方程即可解决问题.
解答: 解:(1)∵OD⊥BC,
解:(1)∵OD⊥BC,
∴BD=DC=0.5,
由勾股定理得:
OD2=OB2-BD2,而OB=2,
∴OD=
.
(2)存在,DE的长度不变.
∵∠AOB=90°,OA=OB=2,
∴AB2=22+22,
∴AB=2
;
∵OD⊥BC,OE⊥AC,
∴BD=DC,AE=CE,
∴DE为△ABC的中位线,
∴DE=
AB=
.
(3)∵OD⊥BC,OE⊥AC,且OA=OB=OC,
∴∠AOE=∠COE(设为α),∠BOD=∠COD(设为β),
∵2(α+β)=90°,
∴α+β=45°,即∠DOE=45°;
设OE=λ;在△DOE中,由余弦定理得:
DE2=OD2+OE2-2OD•OE•cos45°,
即2=3+OE2-2
•OE•
,
整理得:OE2-
OE+1=0,
解得:OE=
或
(舍去).
∴OE=
.
 解:(1)∵OD⊥BC,
解:(1)∵OD⊥BC,∴BD=DC=0.5,
由勾股定理得:
OD2=OB2-BD2,而OB=2,
∴OD=
| ||
| 2 |
(2)存在,DE的长度不变.
∵∠AOB=90°,OA=OB=2,
∴AB2=22+22,
∴AB=2
| 2 |
∵OD⊥BC,OE⊥AC,
∴BD=DC,AE=CE,
∴DE为△ABC的中位线,
∴DE=
| 1 |
| 2 |
| 2 |
(3)∵OD⊥BC,OE⊥AC,且OA=OB=OC,
∴∠AOE=∠COE(设为α),∠BOD=∠COD(设为β),
∵2(α+β)=90°,
∴α+β=45°,即∠DOE=45°;
设OE=λ;在△DOE中,由余弦定理得:
DE2=OD2+OE2-2OD•OE•cos45°,
即2=3+OE2-2
| 3 |
| ||
| 2 |
整理得:OE2-
| 6 |
解得:OE=
| ||||
| 2 |
| ||||
| 2 |
∴OE=
| ||||
| 2 |
点评:该题主要考查了垂径定理、三角形的中位线定理、勾股定理及其应用问题;牢固掌握定理是基础,灵活运用解答是关键.

练习册系列答案
相关题目
下列方程是一元一次方程的是( )
| A、2x+y=1 | ||
B、x+2=
| ||
| C、x2+2x+1=0 | ||
D、2x+
|
火星和地球的距离约为340000000千米,用科学记数法表示340000000的结果是( )
| A、3.4×108千米 |
| B、3.4×105千米 |
| C、34×104 |
| D、3.4×104 |
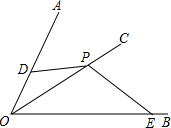 如图,OC平分∠AOB,P是OC上一点,D是OA上一点,E是OB上一点,且PD=PE.求证:∠PDO+∠PEO=180°.
如图,OC平分∠AOB,P是OC上一点,D是OA上一点,E是OB上一点,且PD=PE.求证:∠PDO+∠PEO=180°.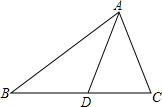 如图,在△ABC中,D是BC上一点,证明:AB+BC+AC>2CD.
如图,在△ABC中,D是BC上一点,证明:AB+BC+AC>2CD. 如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与AB重合)过点P作AB的垂线交BC的延长线于点Q.
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与AB重合)过点P作AB的垂线交BC的延长线于点Q.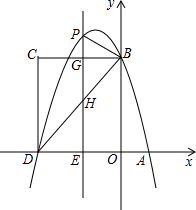 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是正方形.点B坐标为(0,4),已知点E(m,0)是线段DO上的动点(m<0),过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是正方形.点B坐标为(0,4),已知点E(m,0)是线段DO上的动点(m<0),过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.