题目内容
 如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与AB重合)过点P作AB的垂线交BC的延长线于点Q.
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与AB重合)过点P作AB的垂线交BC的延长线于点Q.(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由;
(2)若BP=6,AP=1,QP=8,求QC的长.
考点:切线的判定
专题:
分析:(1)连结OC,由OC=OB得∠2=∠B,DQ=DC得∠1=∠Q,根据QP⊥PB得到∠Q+∠B=90°,则∠1+∠2=90°,再利用平角的定义得到∠DCO=90°,然后根据切线的判定定理得到CD为⊙O的切线;
(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据勾股定理求得BQ、BC,然后根据三角形相似的性质求得BC,最后利用QC=BQ-BC进行计算即可.
(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据勾股定理求得BQ、BC,然后根据三角形相似的性质求得BC,最后利用QC=BQ-BC进行计算即可.
解答:(1)解:CD与⊙O相切.理由如下:如图,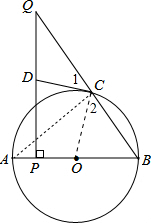
∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°-∠1-∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)解:连接AC,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△BPQ中,BQ=
=
=10,
∵∠ACB=∠QPB=90°,∠ABC=∠QPB,
∴△ABC∽△QBP,
∴
=
,
∵AB=AP+BP=1+6=7,
∴
=
,
∴BC=4.2,
∴QC=BQ-BC=10-4.2=5.8.

∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°-∠1-∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)解:连接AC,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△BPQ中,BQ=
| QP2+BP2 |
| 82+62 |
∵∠ACB=∠QPB=90°,∠ABC=∠QPB,
∴△ABC∽△QBP,
∴
| BC |
| BP |
| AB |
| BQ |
∵AB=AP+BP=1+6=7,
∴
| BC |
| 6 |
| 7 |
| 10 |
∴BC=4.2,
∴QC=BQ-BC=10-4.2=5.8.
点评:本题考查了切线的判定和勾股定理的应用,切线的判定定理是:过半径的外端点与半径垂直的直线为圆的切线.也考查等腰三角形的性质以及三角形相似的判定和性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
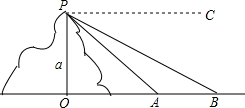 小强在山顶P处观测到有一河流,如图所示,设山的高度OP=a米,A、B分别是河两岸上的点,且A、B、O三点共线.从P点测得点A的俯角为α,点B的俯角为β,求河流的宽AB.
小强在山顶P处观测到有一河流,如图所示,设山的高度OP=a米,A、B分别是河两岸上的点,且A、B、O三点共线.从P点测得点A的俯角为α,点B的俯角为β,求河流的宽AB.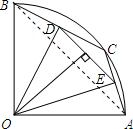 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为O,E.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为O,E. 如图,已知双曲线y=
如图,已知双曲线y=
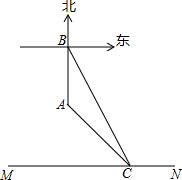 如图,某数学星期小组为了测量一东西走向的小河的宽度,设计了如下测量方案,先在北岸A处测得南岸一目标C在其东南方向,再向正北方向走50米到达B处,又测得目标C在其南偏东30°方向,请你根据以上测量结果计算小河的宽度(结果用根号表示).
如图,某数学星期小组为了测量一东西走向的小河的宽度,设计了如下测量方案,先在北岸A处测得南岸一目标C在其东南方向,再向正北方向走50米到达B处,又测得目标C在其南偏东30°方向,请你根据以上测量结果计算小河的宽度(结果用根号表示).