题目内容
解方程:
(1)x2-8x+15=O;
(2)x2+6x=7;
(3)x(x-4)=-3;
(4)-x2+7x-3=0;
(5)3x2+2x2-l=O;
(6)x2-
x+
=0;
(7)2x2+x-4=0;
(8)(2y+1)2+l5=8(2y+1).
(1)x2-8x+15=O;
(2)x2+6x=7;
(3)x(x-4)=-3;
(4)-x2+7x-3=0;
(5)3x2+2x2-l=O;
(6)x2-
| 1 |
| 3 |
| 1 |
| 6 |
(7)2x2+x-4=0;
(8)(2y+1)2+l5=8(2y+1).
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)根据十字相乘法解答;
(2)利用十字相乘法解答;
(3)利用十字相乘法解答;
(4)利用公式法解答;
(5)利用十字相乘法解答;
(6)利用公式法解答;
(7)利用公式法解答;
(8)利用十字相乘法解答.
(2)利用十字相乘法解答;
(3)利用十字相乘法解答;
(4)利用公式法解答;
(5)利用十字相乘法解答;
(6)利用公式法解答;
(7)利用公式法解答;
(8)利用十字相乘法解答.
解答:解:(1)x2-8x+15=O;
因式分解得(x-3)(x-5)=0,
解得x1=3,x2=5.
(2)x2+6x=7;
方程化为x2+6x-7=0,
因式分解得(x-1)(x+7)=0,
解得x1=1,x2=-7.
(3)x(x-4)=-3;
方程化为x2-4x+3=0,
(x-1)(x-3)=0,
解得x1=1,x2=3.
(4)-x2+7x-3=0;
方程化为x2-7x+3=0;
a=1,b=-7,c=3,
△=49-4×1×3=37,
x1=
,x2=
.
(5)3x2+2x2-l=O;
因式分解得(x+1)(3x-1)=0,
x1=-1,x2=
.
(6)x2-
x+
=0;
方程化为6x2-2x+1=0;
a=6,b=-2,c=1,
△=4-4×6<0,
方程无解.
(7)2x2+x-4=0;
a=2,b=1,c=-4,
△=1-4×2×(-4)=33,
x1=
,x2=
.
(8)(2y+1)2+l5=8(2y+1);
方程化为(2y+1)2-8(2y+1)+l5=0;
因式分解得(2y+1-3)(2y+1-5)=0,
解得y1=1,y2=2.
因式分解得(x-3)(x-5)=0,
解得x1=3,x2=5.
(2)x2+6x=7;
方程化为x2+6x-7=0,
因式分解得(x-1)(x+7)=0,
解得x1=1,x2=-7.
(3)x(x-4)=-3;
方程化为x2-4x+3=0,
(x-1)(x-3)=0,
解得x1=1,x2=3.
(4)-x2+7x-3=0;
方程化为x2-7x+3=0;
a=1,b=-7,c=3,
△=49-4×1×3=37,
x1=
7+
| ||
| 2 |
7-
| ||
| 2 |
(5)3x2+2x2-l=O;
因式分解得(x+1)(3x-1)=0,
x1=-1,x2=
| 1 |
| 3 |
(6)x2-
| 1 |
| 3 |
| 1 |
| 6 |
方程化为6x2-2x+1=0;
a=6,b=-2,c=1,
△=4-4×6<0,
方程无解.
(7)2x2+x-4=0;
a=2,b=1,c=-4,
△=1-4×2×(-4)=33,
x1=
-1+
| ||
| 4 |
-1-
| ||
| 4 |
(8)(2y+1)2+l5=8(2y+1);
方程化为(2y+1)2-8(2y+1)+l5=0;
因式分解得(2y+1-3)(2y+1-5)=0,
解得y1=1,y2=2.
点评:本题考查了一元二次方程的解法,要熟悉各种解法,灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算x(2x-1)-x(2-x)的结果正确的是( )
| A、x2-x |
| B、3x2-3x |
| C、3x2+3x |
| D、x2-3x |
下列说法不正确的是( )
| A、抽样调查时被调查的对象不能太少 |
| B、抽样调查时,样本的选取应具有随机性 |
| C、只要样本容量大就一定能保证调查结果准确 |
| D、抽样调查的优点是调查的范围小,节省时间、人力、物力 |
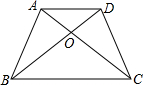 如图,在四边形ABCD中,AC与BD相交于点O,如果△ABO≌△DCO,试在图中再找出一对全等三角形,并加以证明.
如图,在四边形ABCD中,AC与BD相交于点O,如果△ABO≌△DCO,试在图中再找出一对全等三角形,并加以证明.