题目内容
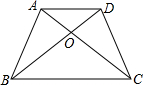 如图,在四边形ABCD中,AC与BD相交于点O,如果△ABO≌△DCO,试在图中再找出一对全等三角形,并加以证明.
如图,在四边形ABCD中,AC与BD相交于点O,如果△ABO≌△DCO,试在图中再找出一对全等三角形,并加以证明.考点:全等三角形的判定与性质
专题:开放型
分析:根据全等三角形的性质由△ABO≌△DCO得到AB=DC,OB=OC,∠ABO=∠DCO,再利用等腰三角形的性质得∠OBC=∠OCB,则有∠ABC=∠DCB,然后根据“SAS”可证得△ABC≌△DCB.
解答:解:△ABC≌△DCB.理由如下:
∵△ABO≌△DCO,
∴AB=DC,OB=OC,∠ABO=∠DCO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC+∠ABO=∠OCB+∠DCO,即∠ABC=∠DCB,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS).
∵△ABO≌△DCO,
∴AB=DC,OB=OC,∠ABO=∠DCO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC+∠ABO=∠OCB+∠DCO,即∠ABC=∠DCB,
在△ABC和△DCB中,
|
∴△ABC≌△DCB(SAS).
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰三角形的性质.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
不等式6-3x<0的最小整数解是( )
| A、3 | B、2 | C、1 | D、0 |
一个数的相反数是非负数,这个数一定是( )
| A、正数或零 | B、非零的数 |
| C、负数或零 | D、零 |
在一次数学考试中,七年级(1)班20名男生平均得m分,26名女生平均得n分,则这个班全体同学的平均分是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
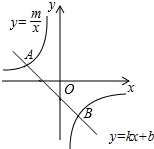 如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y=
如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y= 已知梯形ABCD的中位线长为4.5,AC、BD交于点O,且BD平分∠ABC,CA平分∠BCD,
已知梯形ABCD的中位线长为4.5,AC、BD交于点O,且BD平分∠ABC,CA平分∠BCD,