题目内容
7.某校租了若干辆车搭载学生外出春游,若每辆车搭载35人,则有27人没有车坐,若每辆车搭载40人,则最后一辆未坐满,但不少于34人.求学校一共租了几辆车?一共有多少学生?分析 设学校一共租了x辆车,则一共有学生(35x+27)人,依据条件“每辆车搭载40人,则最后一辆未坐满,但不少于34人”列出不等式组解答即可
解答 解:设学校一共租了x辆车,则一共有学生(35x+27)人. 由题意可知:
$\left\{\begin{array}{l}{35x+27-40(x-1)<40}\\{35x+27-40(x-1)≥34}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x>5\frac{2}{5}}\\{x≤6\frac{3}{5}}\end{array}\right.$,
∴5$\frac{2}{5}$<x≤6$\frac{3}{4}$
∴x的整数解为x=6,
∴35x+27=237
答:学校一共租了6辆车,一共有学生237人.
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.

练习册系列答案
相关题目
2.根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | 0.06 | 0.02 | 0.03 | 0.09 |
| A. | 3<x<3.23 | B. | 3.23<x<3.24 | C. | 3.24<x<3.25 | D. | 3.25<x<3.26 |
19.某商场经销甲、乙两种商品,甲种商品每件进价20元,售价35元;乙种商品每件进价30元,售价50元.
(1)若该商场同时购进甲、乙两种商品共100件,且使这100件商品的总利润(利润=售价-进价)为1800元,需购进甲、乙两种商品各多少件?
(2)在“十一”期间,该商场对甲、乙两种商品进行如下优惠促销活动:
按上述优惠条件,若小李第一天只购买甲种商品一次性付款210元,第二天只购买乙种商品打折后一次性付款440元,那么这两天他在该商场购买甲、乙两种商品一共多少件?
(1)若该商场同时购进甲、乙两种商品共100件,且使这100件商品的总利润(利润=售价-进价)为1800元,需购进甲、乙两种商品各多少件?
(2)在“十一”期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过500元 | 售价一律打九折 |
| 超过500元 | 售价一律打八折 |
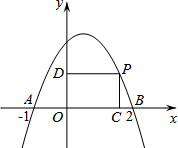 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(2,0).点P是x轴上方抛物线上一动点(不落在y轴上),过点P作PD∥x轴交y轴于点D.PC∥y轴交x轴于点C,设点P的横坐标为m,矩形PDOC的周长为L.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(2,0).点P是x轴上方抛物线上一动点(不落在y轴上),过点P作PD∥x轴交y轴于点D.PC∥y轴交x轴于点C,设点P的横坐标为m,矩形PDOC的周长为L.