题目内容
19.某商场经销甲、乙两种商品,甲种商品每件进价20元,售价35元;乙种商品每件进价30元,售价50元.(1)若该商场同时购进甲、乙两种商品共100件,且使这100件商品的总利润(利润=售价-进价)为1800元,需购进甲、乙两种商品各多少件?
(2)在“十一”期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过500元 | 售价一律打九折 |
| 超过500元 | 售价一律打八折 |
分析 (1)等量关系为:甲商品总进价+乙商品总进价=1800,根据此关系列方程即可求解.
(2)第一天的总价为210元,所以没有享受打折,第二天的也可能享受了9折,也可能享受了8折.应先算出原价,然后除以单价,得出数量.
解答 解:(1)设该商场购进甲种商品a件,则购进乙种商品(100-a)件.根据题意得
(35-20)a+(50-3 0)(100-a)=1800,
解得,a=40,100-a=60,
答:需购进甲、乙两种商品各40,60件;
(2)根据题意得,第一天只购买甲种商品不享受优惠条件
∴210÷35=6 (件),
第二天只购买乙种商品有以下两种可能:
①:若购买乙商品打九折,440÷90%÷50=$\frac{88}{9}$(件),不符合实际,舍去;
②:购买乙商品打八折,440÷80%÷50=11(件),
∴一共可购买甲、乙两种商品6+11=17(件).
点评 此题考查一元一次方程的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式组,及所求量的等量关系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
14.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  等边三角形 | B. |  平行四边形 | C. |  正五边形 | D. |  正六边形 |
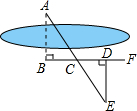 如图所示,要测量河两岸上对岸两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再在BF的垂线DE上取点E,使A、C、E在同一条直线上,可以得到△ABC≌△EDC,得DE=AB,因此测得ED的长就是AB的长,判定△ABC≌△EDC的理由是( )
如图所示,要测量河两岸上对岸两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再在BF的垂线DE上取点E,使A、C、E在同一条直线上,可以得到△ABC≌△EDC,得DE=AB,因此测得ED的长就是AB的长,判定△ABC≌△EDC的理由是( )