题目内容
13．已知P、Q是线段AB的两个黄金分割点，且AB=10，则PQ长为（ ）| A． | $5\sqrt{5}-5$ | B． | $5\sqrt{5}+1$ | C． | 10$\sqrt{5}$-20 | D． | $15-5\sqrt{5}$ |
分析 根据黄金比是$\frac{\sqrt{5}-1}{2}$进行计算即可．
解答 解：
∵P是线段AB的黄金分割点，
∴AQ=$\frac{\sqrt{5}-1}{2}$AB=5$\sqrt{5}$-5，
Q是线段AB的两个黄金分割点，
∴BP=$\frac{\sqrt{5}-1}{2}$AB=5$\sqrt{5}$-5，
∴PQ=AQ+BP-AB=10$\sqrt{5}$-20，
故选：C．
点评 本题考查的是黄金分割的概念，掌握把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比是解题的关键．
练习册系列答案
快乐5加2金卷系列答案
相关题目
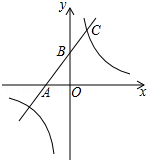如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数y=$\frac{k}{x}$（k≠0）的图象在第一象限交于点C，如果点B的坐标为（0，2），OA=OB，B是线段AC的中点．