题目内容
4.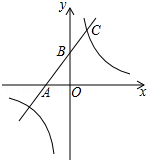 如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.(1)求一次函数解析式及反比例函数的解析式;
(2)若一次函数值大于反比例函数值,请求出相应的自变量x的取值范围.
分析 (1)根据条件可先求得A点坐标,再根据中点,可求得C点坐标,然后根据待定系数法即可求得一次函数解析式及反比例函数的解析式;
(2)根据交点坐标和函数的图象即可求得.
解答 解:(1)∵OA=OB,点B的坐标为(0,2),
∴点A(-2,0),点A、B在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}{-2k+b=0}\\{b=2}\end{array}\right.$,解得k=1,b=2,
∴一次函数的解析式为y=x+2.
∵B是线段AC的中点,
∴点C的坐标为(2,4),
又∵点C在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=8
∴反比例函数的解析式为y=$\frac{8}{x}$.
(2)一次函数值大于反比例函数值的自变量x的取值范围-4<x<0或x>2.
点评 本题主要考查了待定系数法求反比例函数与一次函数的解析式.这里体现了数形结合的思想.

练习册系列答案
相关题目
19.已知点P(3,-2)与点Q关于y轴对称,则点Q的坐标为( )
| A. | (-3,2) | B. | (-3,-2) | C. | (3,2) | D. | (3,-2) |
16.冬季某天我国三个城市的最高气温分别是-11℃,3℃,-3℃,它们任意两城市中最大的温差是( )
| A. | 11℃ | B. | 13℃ | C. | 14℃ | D. | 6℃ |
13.已知P、Q是线段AB的两个黄金分割点,且AB=10,则PQ长为( )
| A. | $5\sqrt{5}-5$ | B. | $5\sqrt{5}+1$ | C. | 10$\sqrt{5}$-20 | D. | $15-5\sqrt{5}$ |
14.若分式$\frac{{x}^{2}-4}{x-2}$的值为0,则x的取值为( )
| A. | x=2 | B. | x=-2 | C. | x=2 | D. | 无法确定 |
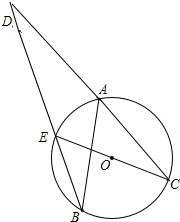 如图,AB、AC是⊙O相等的两弦,延长CA至点D,使AD=AC,连接DB交⊙O于点E,连接CE.证明:CE是⊙O的直径.
如图,AB、AC是⊙O相等的两弦,延长CA至点D,使AD=AC,连接DB交⊙O于点E,连接CE.证明:CE是⊙O的直径.